Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-15T01:46:50.849Z Has data issue: false hasContentIssue false
  • English
  • Français

On Toda's fibrations

Published online by Cambridge University Press:  24 October 2008

Brayton Gray
Brayton Gray
Affiliation:
Department of Mathematics, University of Illinois at Chicago
Get access Rights & Permissions [Opens in a new window]

Extract

In 1956 Toda [5] introduced two fibrations localized at p > 2:

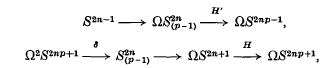
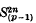where is a subcomplex of the James construction 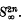. The construction of H′ was somewhat difficult and was discussed by Moore (see [3]). Moore's definition however is not natural (in the sense of Theorem 1 (b) below). It is our purpose to give another definition, closer to Toda's original definition, which is natural, is an H map* and behaves well with respect to the Dyer-Lashof map λ: BΣp → Q(So). We use this to settle an unanswered question in [2].

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 97 , Issue 2 , March 1985 , pp. 289 - 298
Copyright
Copyright © Cambridge Philosophical Society 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Gray, B.. On the homotopy groups of mapping cones. Proc. London Math. Soc. (3) 26 (1973), 497–520.CrossRefGoogle Scholar
[2]Gray, B.. Unstable families related to the image of J. Math. Proc. Cambridge Philos. Soc. 96 (1984), 95–113.CrossRefGoogle Scholar
[3]Selick, P.. A spectral sequence concerning the double suspension. Invent. Math. 64 (1981), 15–24.CrossRefGoogle Scholar
[4]Serre, J. P.. Cohomologie modulo 2 des complexes d'eilenberg-MacLane. Comment. Math. Helv. 27 (1953), 198–232.CrossRefGoogle Scholar
[5]Toda, H.. On the double suspension E2. J. Inst. Polytech. Osaka City Univ. 7 (1956) 103–145.Google Scholar