On ‘translated quasi-Cesàro’ summability. II
Published online by Cambridge University Press: 24 October 2008
Extract
In a recent paper (1), I considered the summability method (D, α) defined, for α > 0, by the sequence-to-sequence transformation
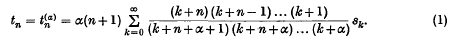
We note that, as is easily verified (and as was pointed out in (1)) a necessary and sufficient condition for the convergence of (1), and thus for the applicability of (D, α), is that

should converge. It was proved in (1) that, provided that (2) converges, a sequence summable (C, r) for any r > − 1 is necessarily summable (D, α). We now show that we can strengthen this result by replacing Cesàro by Abel summability. Moreover, we can omit the hypothesis that (2) converges provided that we interpret (1) as an Abel sum.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 66 , Issue 1 , July 1969 , pp. 39 - 41
- Copyright
- Copyright © Cambridge Philosophical Society 1969
References
REFERENCE
- 1
- Cited by


