Published online by Cambridge University Press: 24 October 2008
Corresponding to a fixed sequence {μn}, the Hausdorff method of summability (H, μn) is defined by the sequence-to-sequence transformation†

where we write
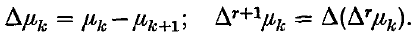
The quasi-Hausdorff method (H*, μn) is defined by the transformation

thus the matrix of the (H*, μn) transformation is the transpose of that of the (H*, μn) transformation. A method introduced by Ramanujan (9), which we will call‡ (S,μn) is given by the transformation
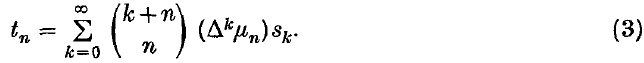
Thus the elements of row n of the matrix of the (S, μn) transformation are those of the corresponding row of the (H*, μn) transformation moved n places to the left.