Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-14T22:28:11.538Z Has data issue: false hasContentIssue false
  • English
  • Français

On Waring's problem for cubes and biquadrates. II

Published online by Cambridge University Press:  24 October 2008

Jörg Brüdern
Jörg Brüdern
Affiliation:
Geismar Landstrasse 97, 34 Göttingen, West Germany
Get access Rights & Permissions [Opens in a new window]

Extract

In discussing the consequences of a conditional estimate for the sixth moment of cubic Weyl sums, Hooley [4] established asymptotic formulae for the number ν(n) of representations of n as the sum of a square and five cubes, and for ν(n), defined similarly with six cubes and two biquadrates. The condition here is the truth of the Riemann Hypothesis for a certain Hasse–Weil L-function. Recently Vaughan [8] has shown unconditionally 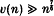, a lower bound of the size suggested by the conditional asymptotic formula. In the corresponding problem for ν(n) the author [1] was able to deduce ν(n) > 0, as a by-product of the result that almost all numbers can be expressed as the sum of three cubes and one biquadrate. As promised in the first paper of this series we return to the problem of bounding ν(n) from below.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 104 , Issue 2 , September 1988 , pp. 199 - 206
Copyright
Copyright © Cambridge Philosophical Society 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Brüdern, J.. On Waring's problem for cubes and biquadrates. J. London Math. Soc. (2) 37 (1988), 25–42.Google Scholar
[2]Brüdern, J.. A problem in additive number theory. Math. Proc. Cambridge Philos. Soc. 103 (1988), 27–33.CrossRefGoogle Scholar
[3]Davenport, H.. On sums of positive integral k-th powers. Amer. J. Math. 64 (1942), 189–198.Google Scholar
[4]Hooley, C.. On Waring's problem. Acta Math. 157 (1986), 49–97.Google Scholar
[5]Thanigasalam, K.. On sums of mixed powers. Bull. Calcutta Math. Soc. 77 (1985), 17–19.Google Scholar
[6]Vaughan, R. C.. The Hardy–Littlewood Method (Cambridge University Press, 1981).Google Scholar
[7]Vaughan, R. C.. On Waring's problem for cubes. J. reine angew. Math. 365 (1986), 122–170.Google Scholar
[8]Vaughan, R. C.. On Waring's problem: one square and five cubes. Quart. J. Math. Oxford Ser. (2) 37 (1986), 117–127.Google Scholar
[9]Vaughan, R. C.. On Waring's problem for smaller exponents. Proc. London Math. Soc. (3) 52 (1986), 445–463.Google Scholar