Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gogyan, Smbat
2009.
On convergence of Weak Thresholding Greedy Algorithm in L1(0,1).
Journal of Approximation Theory,
Vol. 161,
Issue. 1,
p.
49.


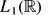 the Haar wavelet basis is not equivalent to any permutation with any signs of the Strω wavelet basis. We also construct a Haar-type system in
the Haar wavelet basis is not equivalent to any permutation with any signs of the Strω wavelet basis. We also construct a Haar-type system in 