Published online by Cambridge University Press: 24 October 2008
Let F be a closed connected and non-orientable surface smoothly embedded in the 4-sphere S4 with normal Euler number e(F) = 0. We note that if e(F) = 0, then the non-orientable genus n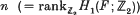 is even (ef. [7]) and the tubular neighbourhood N(F) of F in S4 which is a D2-bundle over F has a trivial I-subbundle. Let τ be a trivial I-subbundle of N(F) and let τ* = F × I ⊂ N(F) be its orthogonal I-subbundle which is twisted. Then
is even (ef. [7]) and the tubular neighbourhood N(F) of F in S4 which is a D2-bundle over F has a trivial I-subbundle. Let τ be a trivial I-subbundle of N(F) and let τ* = F × I ⊂ N(F) be its orthogonal I-subbundle which is twisted. Then 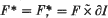 is a closed connected genus n – 1 orientable surface smoothly embedded in S4 and doubly covers F. We call this surface a doubled surface of F in S4 (associated with τ). If a trivial I-subbundle τ is given, then we see that the knot type of F* ⊂ S4 is uniquely determined.
is a closed connected genus n – 1 orientable surface smoothly embedded in S4 and doubly covers F. We call this surface a doubled surface of F in S4 (associated with τ). If a trivial I-subbundle τ is given, then we see that the knot type of F* ⊂ S4 is uniquely determined.