Article contents
Overstable convection in a horizontally heated rotating fluid
Published online by Cambridge University Press: 24 October 2008
Abstract
Fluid is contained in a rotating annulus of rectangular cross-section which is subject to a radial temperature gradient along the base and is insulated around its upper surfaces. If E is an Ekman number, which is assumed small, a finite amplitude cellular motion of wavelength ∼ E⅓ develops near the inner sidewall of the annulus by an exchange process if the local Rayleigh number, R, exceeds its critical value Rc and the Prandtl number of the fluid, σ, is greater than a critical value, σc (Daniels and Stewartson(5)). In the present study we consider the remaining range of values 0 < σ < σc for which overstability is preferred, occurring at a value of the Rayleigh number, Rc0, less than Rc. Disturbances to the basic flow near the sidewall now oscillate in time with frequency ∼ E⅓ and are amplified if R exceeds Rc0, the vertical cellular velocity attaining values ∼ E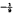 in a region of extent ∼ E
in a region of extent ∼ E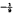 near the sidewall. On the time-scale ∼ E
near the sidewall. On the time-scale ∼ E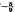 disturbances take the form of two wave-like components which travel in opposite directions with the characteristic group velocity of the system. The first is simply convected away from the sidewall into the stably stratified interior and decays, while the second travels towards the sidewall where it is reflected. The reflexion coefficient is determined by the dynamics of an E⅓ boundary layer where an oscillatory motion is generated by the incident wave.
disturbances take the form of two wave-like components which travel in opposite directions with the characteristic group velocity of the system. The first is simply convected away from the sidewall into the stably stratified interior and decays, while the second travels towards the sidewall where it is reflected. The reflexion coefficient is determined by the dynamics of an E⅓ boundary layer where an oscillatory motion is generated by the incident wave.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 83 , Issue 2 , March 1978 , pp. 329 - 345
- Copyright
- Copyright © Cambridge Philosophical Society 1978
References
REFERENCES
- 2
- Cited by


