Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-24T06:18:01.790Z Has data issue: false hasContentIssue false
  • English
  • Français

The packing measure of the graphs and level sets of certain continuous functions

Published online by Cambridge University Press:  24 October 2008

Fraydoun Rezakhanlou
Fraydoun Rezakhanlou
Affiliation:
Courant Institute of Mathematical Sciences, New York University, New York, NY 10012, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

The relationship between the local growth of a continuous function and the packing measure of its level sets and of its graph is studied. For the Weierstrass function 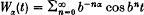with b an integer such that b ≥ 2 and with 0 < α < 1, and for x ∈ Range (W) outside a set of first category, the level set W−1(x) has packing dimension at least 1 − α. Furthermore, for almost all x ∈ Range (W), the packing dimension of f is at most 1 − α. Finer results on the occupation measure and the size of the graph of a continuous function satisfying the Zygmund Λ-condition are obtained.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 104 , Issue 2 , September 1988 , pp. 347 - 360
Copyright
Copyright © Cambridge Philosophical Society 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Anderson, J. M. and Pitt, L. D.. Probabilistic Behavior of Functions in the Zygmund Spaces Λ* and λ*. (Preprint.)Google Scholar
[2]Berry, M. V. and Lewis, Z. V.. On the Weierstrass–Mandelbrot fractal function. Proc. Roy. Soc. London Ser. A 370 (1980), 459–484.Google Scholar
[3]Besicovitch, A. S. and Ursell, H. D.. Sets of fractional dimensions, V: On dimensional numbers of some continuous curves. J. London Math. Soc. 12 (1937), 18–25.CrossRefGoogle Scholar
[4]Falconer, K. J.. The Geometry of Fractal Sets (Cambridge University Press, 1985).CrossRefGoogle Scholar
[5]Izumi, M., Izumi, S.-I. and Kahane, J.-P.. Théorèmes elementaires sur les séries de Fourier lacunaires. J. Analyse Math. 14 (1965), 235–246.CrossRefGoogle Scholar
[6]Kahane, J.-P.. Geza Freud and lacunary Fourier series. J. Approx. Theory 46 (1986), 51–57.CrossRefGoogle Scholar
[7]Marstrand, J. M.. The dimension of cartesian product sets. Proc. Cambridge Philos. Soc. 50 (1954), 198–202.CrossRefGoogle Scholar
[8]Mauldin, R. D. and Williams, S. C.. On the Hausdorff dimension of some graphs. Trans. Amer. Math. Soc. 298 (1986), 793–803.CrossRefGoogle Scholar
[9]Orey, S. and Taylor, S. J.. How often on a Brownian path does the law of iterated logarithm fail? Proc. London Math. Soc. 28 (1974), 174–192.CrossRefGoogle Scholar
[10]Rezakhanlou, F. and Taylor, S. J.. The packing measure of the graph of a stable process. (Preprint.)Google Scholar
[11]Rogers, C. A.. Hausdorff Measures (Cambridge University Press, 1970).Google Scholar
[12]Taylor, S. J.. The measure theory of random fractals. Math. Proc. Cambridge Philos. Soc. 100 (1986), 383–406.CrossRefGoogle Scholar
[13]Taylor, S. J.. The use of packing measure in the analysis of random sets. In Proceedings of the 15th Symposium on Stochastic Processes and Applications, Lecture Notes in Math. vol. 1203 (Springer-Verlag, 1986), pp. 214–222.CrossRefGoogle Scholar
[14]Taylor, S. J. and Tricot, C.. Packing measure, and its evaluation for a Brownian path. Trans. Amer. Math. Soc. 288 (1985), 679–699.CrossRefGoogle Scholar
[15]Zygmund, A.. Trigonometric Series, 2nd edn. (Cambridge University Press, 1959).Google Scholar