No CrossRef data available.
Published online by Cambridge University Press: 05 April 2018
Let K be a field of characteristic 0. Fix integers r, d coprime with r ⩾ 2. Let XK be a smooth, projective, geometrically connected curve of genus g ⩾ 2 defined over K. Assume there exists a line bundle 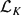 ${\cal L}_K$ on XK of degree d. In this paper we prove the existence of a stable locally free sheaf on XK with rank r and determinant
${\cal L}_K$ on XK of degree d. In this paper we prove the existence of a stable locally free sheaf on XK with rank r and determinant 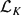 ${\cal L}_K$. This trivially proves the C1 conjecture in mixed characteristic for the moduli space of stable locally free sheaves of fixed rank and determinant over a smooth, projective curve.
${\cal L}_K$. This trivially proves the C1 conjecture in mixed characteristic for the moduli space of stable locally free sheaves of fixed rank and determinant over a smooth, projective curve.