Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zachariou, A.
1967.
A subalgebra of 𝐸𝑥𝑡_{𝐴}**(𝑍₂,𝑍₂).
Bulletin of the American Mathematical Society,
Vol. 73,
Issue. 5,
p.
647.
Mahowald, Mark
1967.
On the order of the image of J.
Topology,
Vol. 6,
Issue. 3,
p.
371.
Mahowald, Mark
1968.
On the metastable homotopy of 𝑂(𝑛).
Proceedings of the American Mathematical Society,
Vol. 19,
Issue. 3,
p.
639.
Moss, R. Michael F.
1970.
Secondary compositions and the Adams spectral sequence.
Mathematische Zeitschrift,
Vol. 115,
Issue. 4,
p.
283.
Zahler, Raphael
1971.
The Adams-Novikov spectral sequence for the spheres.
Bulletin of the American Mathematical Society,
Vol. 77,
Issue. 1,
p.
169.
Margolis, Harvey
Priddy, Stewart
and
Tangora, Martin
1971.
Another systematic phenomenon in the cohomology of the Steenrod algebra.
Topology,
Vol. 10,
Issue. 1,
p.
43.
Fuks, D. B.
1973.
Homotopic topology.
Journal of Soviet Mathematics,
Vol. 1,
Issue. 3,
p.
333.
Anderson, Donald W.
and
Davis, Donald W.
1973.
A vanishing theorem in homological algebra.
Commentarii Mathematici Helvetici,
Vol. 48,
Issue. 1,
p.
318.
Lin, Wen-Hsiung
1977.
Cohomology of sub-Hopf-algebras of the Steenrod algebra.
Journal of Pure and Applied Algebra,
Vol. 10,
Issue. 2,
p.
101.
Miller, Haynes R.
1978.
A localization theorem in homological algebra.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 84,
Issue. 1,
p.
73.
Ravenel, Douglas C.
1978.
Geometric Applications of Homotopy Theory II.
Vol. 658,
Issue. ,
p.
404.
Miller, Haynes R.
1981.
On relations between Adams spectral sequences, with an application to the stable homotopy of a moore space.
Journal of Pure and Applied Algebra,
Vol. 20,
Issue. 3,
p.
287.
Miller, Haynes
and
Wilkerson, Clarence
1981.
Vanishing lines for modules over the Steenrod algebra.
Journal of Pure and Applied Algebra,
Vol. 22,
Issue. 3,
p.
293.
Lin, W.-H.
1983.
Cohomology of the Steenrod algebra.
Journal of Pure and Applied Algebra,
Vol. 29,
Issue. 1,
p.
75.
1983.
Spectra and the Steenrod Algebra: Modules over the Steenrod Algebra and the Stable Homotopy Category.
Vol. 29,
Issue. ,
p.
480.
Crabb, M. C.
and
Knapp, K.
1986.
Vector bundles of maximal codegree.
Mathematische Zeitschrift,
Vol. 193,
Issue. 2,
p.
285.
1986.
Vol. 121,
Issue. ,
p.
395.
Mahowald, Mark
and
Shick, Paul
1987.
Periodic phenomena in the classical Adams spectral sequence.
Transactions of the American Mathematical Society,
Vol. 300,
Issue. 1,
p.
191.
Davis, Donald M.
and
Mahowald, Mark
1988.
𝑣₁-periodic 𝐸𝑥𝑡 over the Steenrod algebra.
Transactions of the American Mathematical Society,
Vol. 309,
Issue. 2,
p.
503.
Singer, William M.
1989.
The transfer in homological algebra.
Mathematische Zeitschrift,
Vol. 202,
Issue. 4,
p.
493.
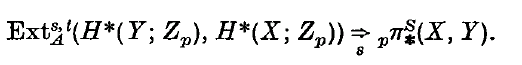
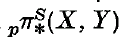 is built up from the E∞ term; these are topological problems.
is built up from the E∞ term; these are topological problems.

