Published online by Cambridge University Press: 24 October 2008
If A = [aij] is an n × n matrix, the permanent of A is the scalar valued function of A defined by
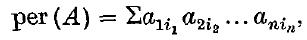
where the summation extends over all permutations (i1, i2, …, in) of the integers 1, 2, …, n. If we assume that A is a non-negative matrix (that is, that A has non-negative entries) then we come upon an extremely interesting situation. Much work has been done in finding significant upper bounds for the permanent and permanental minors of A (see, e.g. (2, 4–7) in (5) an excellent bibliography is given). If B = [bij] is another n × n non-negative matrix, then we may form the product AB and consider the permanent of this matrix. Unlike the determinant, the permanent is not a multiplicative function. In our circumstances here, however, it is easy to verify and indeed a proof was written down in (1) that