Published online by Cambridge University Press: 24 October 2008
First we consider an elementary though delicate question about the trajectory in ℝn of a particle in a conservative field of force whose dynamics are governed by the equation
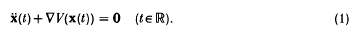
Here the potential function V is supposed to have Lipschitz continuous first derivative at every point of ℝn. This is a natural assumption which ensures that the initial-value problem is well-posed. We suppose also that there is a closed convex set C with non-empty interior C° such that V ≥ 0 in C and V = 0 on the boundary ∂C of C. It is noteworthy that we make no assumptions about the degeneracy (or otherwise) of V on ∂C (i.e. whether ∇V = 0 on ∂C, or not); thus ∂C is a Lipschitz boundary because of its convexity but not necessarily any smoother in general. We remark also that there are no convexity assumptions about V and nothing is known about the behaviour of V outside C.