Properties (V) and (w V) on C(Ω X)
Published online by Cambridge University Press: 24 October 2008
Extract
A formal series Σxn in a Banach space X is said to be weakly unconditionally converging, or alternatively weakly unconditionally Cauchy (wuc) if Σ|x*(xn)| < ∞ for every continuous linear functional x* ∈ X*. A subset K of X* is called a V-subset of X* if
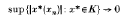
for each wuc series Σxn in X. Further, the Banach space X is said to have property (V) if the V-subsets of X* coincide with the relatively weakly compact subsets of X*. In a fundamental paper in 1962, Pelczynski [10] showed that the Banach space X has property (V) if and only if every unconditionally converging operator with domain X is weakly compact. In this same paper, Pelczynski also showed that all C(Ω) spaces have property (V), and asked if the abstract continuous function space C(Ω, X) has property (F) whenever X has property (F).
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 117 , Issue 3 , May 1995 , pp. 469 - 477
- Copyright
- Copyright © Cambridge Philosophical Society 1995
References
REFERENCES
- 2
- Cited by

