No CrossRef data available.
Published online by Cambridge University Press: 03 February 2012
Unfortunately, there are two inaccuracies in the argument of [CLS]. First, the statements of Lemmas 3, 4, 6, and 7 of [CLS] hold only under the additional condition gcd(m, ME) = 1 for some integer ME ≥ 1 depending only on E. Second, the divisibility condition (3·6) in [CLS] implies that tb(ℓ) | nE(p)−1 (rather than tb(ℓ) | nE(p), as it was erroneously claimed on p. 519 in [CLS]). In particular, instead of the divisibility ℓtb(ℓ) | nE(p) (see the last displayed formula on p. 519 in [CLS]), we conclude that for every prime ℓ | L there is an integer aℓ such that(0.1)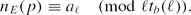 However, the final result is correct and can easily be recovered. To do so, we remark that under the condition gcd(m,ME) =1, we have full analogues of Lemmas 6, 7, 9, and 10 of [CLS] for the function Π(x;m,a) defined as the number of primes p ≤ x with nE(p) ≡ a (mod m) (rather than just for Π(x;m) = Π(x;m,0) as in [CLS]). Define ρ*(n) as the largest square-free divisor of n which is relatively prime to ME. We then derive from (0.1) above that
However, the final result is correct and can easily be recovered. To do so, we remark that under the condition gcd(m,ME) =1, we have full analogues of Lemmas 6, 7, 9, and 10 of [CLS] for the function Π(x;m,a) defined as the number of primes p ≤ x with nE(p) ≡ a (mod m) (rather than just for Π(x;m) = Π(x;m,0) as in [CLS]). Define ρ*(n) as the largest square-free divisor of n which is relatively prime to ME. We then derive from (0.1) above that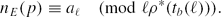 Therefore(0.2)
Therefore(0.2)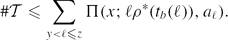 Since
Since we see that (0.2) above implies the bound (3·7) from [CLS], and the result now follows without any further changes.
we see that (0.2) above implies the bound (3·7) from [CLS], and the result now follows without any further changes.