Published online by Cambridge University Press: 24 October 2008
The best of the theorems on continued fractions, to be found in Ramanujan's manuscript note-book may be stated as follows:
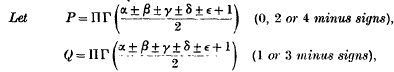
where there are eight gamma-functions in each product and the ambiguous signs are so chosen that the argument of each gamma-function contains one of the specified numbers of minus signs. Then
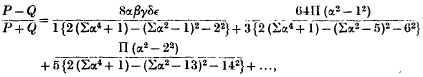
provided that one of the numbers β, γ δ, ε is equal to ± n, where n is a positive integer; and the products and sums on the right range over the numbers α β, γ δ, ε.
* Through an error in copying which occurred when I previously published an enunciation of the theorem, Journal London Math. Soc. 6 (1931), 146Google Scholar, the numbers in b 2 were inadvertently given as 9 and 10 instead of 13 and 14.
† Perron, O.. Die Lehre von den Kettenbrüchen (2. Aufl. 1929)Google Scholar.
* Hardy, G. H., “A chapter from Ramanujan's note-book”, Proc. Camb. Phil. Soc. 21 (1923), 492–503.Google Scholar
† Laguerre, E., “Sur la function ![]() ”, Bull. Soc. Math. France, 8 (1879), 36–52.Google Scholar
”, Bull. Soc. Math. France, 8 (1879), 36–52.Google Scholar
* Here and elsewhere it is supposed that the “numerators” and “denominators” of the convergents of a continued fraction are calculated without cancelling common factors, if such exist. Thus the numerators of the convergents of the continued fraction
are
* The properties of the original expressions show that their difference vanishes when α = 0, and so the difference contains α as a factor; similarly for β, γ, δ. Hence C n (α, β, γ, δ) is an integral function.