Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Saneblidze, Samson
1993.
Obstructions to the section problem in fibre bundles.
manuscripta mathematica,
Vol. 81,
Issue. 1,
p.
95.
Buchstaber, V. M.
and
Rees, E. G.
1997.
Multivalued groups, their representations and Hopf algebras.
Transformation Groups,
Vol. 2,
Issue. 4,
p.
325.
Pejsachowicz, Jacobo
and
Skiba, Robert
2005.
Handbook of Topological Fixed Point Theory.
p.
217.
Aguilar, Marcelo A.
and
Prieto, Carlos
2006.
Transfers for ramified covering maps in homology and cohomology.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2006,
Issue. 1,
Aguilar, Marcelo A.
and
Prieto, Carlos
2008.
Simplicial ramified covering maps.
Topology and its Applications,
Vol. 156,
Issue. 2,
p.
205.
BUCHSTABER, V. M.
BUCHSTABER, V. M.
and
REES, E. G.
2008.
Frobenius n-homomorphisms, transfers and branched coverings.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 144,
Issue. 1,
p.
1.
Neretin, Yu. A.
2010.
On spherical functions on the group SU(2) × SU(2) × SU(2).
Functional Analysis and Its Applications,
Vol. 44,
Issue. 1,
p.
48.
Aguilar, Marcelo A.
and
Prieto, Carlos
2010.
Bredon homology and ramified covering G-maps.
Topology and its Applications,
Vol. 157,
Issue. 2,
p.
401.
Натанзон, Сергей Миронович
Natanzon, Sergey Mironovich
Натанзон, Сергей Миронович
Natanzon, Sergey Mironovich
Натанзон, Сергей Миронович
Natanzon, Sergey Mironovich
Натанзон, Сергей Миронович
and
Natanzon, Sergey Mironovich
2010.
Дисковые одинарные числа Гурвица.
Функциональный анализ и его приложения,
Vol. 44,
Issue. 1,
p.
44.
Natanzon, S. M.
2010.
Simple Hurwitz numbers of a disk.
Functional Analysis and Its Applications,
Vol. 44,
Issue. 1,
p.
36.
Gugnin, D. V.
2018.
Lower Bounds for the Degree of a Branched Covering of a Manifold.
Mathematical Notes,
Vol. 103,
Issue. 1-2,
p.
187.
Gugnin, Dmitry Vladimirovich
2018.
О нижних оценках на степень разветвленных накрытий многообразий.
Математические заметки,
Vol. 103,
Issue. 2,
p.
186.
Gugnin, D. V.
2019.
Branched Coverings of Manifolds and nH-Spaces.
Functional Analysis and Its Applications,
Vol. 53,
Issue. 2,
p.
133.
Gugnin, Dmitry Vladimirovich
2019.
Разветвленные накрытия многообразий и $\boldsymbol{nH}$-пространства.
Функциональный анализ и его приложения,
Vol. 53,
Issue. 2,
p.
68.
Buchstaber, Victor Matveevich
Veselov, Aleksandr Petrovich
and
Gaifullin, Alexander Aleksandrovich
2022.
Классификация инволютивных коммутативных двузначных групп.
Успехи математических наук,
Vol. 77,
Issue. 4(466),
p.
91.
Buchstaber, Victor Matveevich
Veselov, Aleksandr Petrovich
and
Gaifullin, Alexander Aleksandrovich
2022.
Classification of involutive commutative two-valued groups.
Russian Mathematical Surveys,
Vol. 77,
Issue. 4,
p.
651.
Buchstaber, Victor Matveevich
and
Vesnin, Andrei Yurievich
2024.
$n$-значные группы, разветвленные накрытия и трехмерные гиперболические многообразия.
Математический сборник,
Vol. 215,
Issue. 11,
p.
3.
Buchstaber, Victor Matveevich
and
Vesnin, Andrei Yurievich
2024.
$n$-valued groups, branched coverings and hyperbolic 3-manifolds.
Sbornik: Mathematics,
Vol. 215,
Issue. 11,
p.
1441.


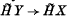 .
.