No CrossRef data available.
Published online by Cambridge University Press: 13 January 2025
The q-colour Ramsey number of a k-uniform hypergraph H is the minimum integer N such that any q-colouring of the complete k-uniform hypergraph on N vertices contains a monochromatic copy of H. The study of these numbers is one of the central topics in Combinatorics. In 1973, Erdős and Graham asked to maximise the Ramsey number of a graph as a function of the number of its edges. Motivated by this problem, we study the analogous question for hypergaphs. For fixed 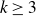 $k \ge 3$ and
$k \ge 3$ and  $q \ge 2$ we prove that the largest possible q-colour Ramsey number of a k-uniform hypergraph with m edges is at most
$q \ge 2$ we prove that the largest possible q-colour Ramsey number of a k-uniform hypergraph with m edges is at most 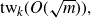 $\mathrm{tw}_k(O(\sqrt{m})),$ where tw denotes the tower function. We also present a construction showing that this bound is tight for
$\mathrm{tw}_k(O(\sqrt{m})),$ where tw denotes the tower function. We also present a construction showing that this bound is tight for  $q \ge 4$. This resolves a problem by Conlon, Fox and Sudakov. They previously proved the upper bound for
$q \ge 4$. This resolves a problem by Conlon, Fox and Sudakov. They previously proved the upper bound for 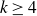 $k \geq 4$ and the lower bound for
$k \geq 4$ and the lower bound for 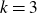 $k=3$. Although in the graph case the tightness follows simply by considering a clique of appropriate size, for higher uniformities the construction is rather involved and is obtained by using paths in expander graphs.
$k=3$. Although in the graph case the tightness follows simply by considering a clique of appropriate size, for higher uniformities the construction is rather involved and is obtained by using paths in expander graphs.
Research supported in part by SNSF grant 200021-228014.
Research supported by NSF Awards DMS-1953990 and DMS-2154129.