Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T21:48:07.845Z Has data issue: false hasContentIssue false
  • English
  • Français

Random fractals and their intersection with winning sets

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Graph theory Markov processes Smooth dynamical systems: general theory Geometric probability and stochastic geometry Classical measure theory

Published online by Cambridge University Press:  07 July 2021

YIFTACH DAYAN
YIFTACH DAYAN*
Affiliation:
Department of Mathematics, Tel Aviv University, Tel-Aviv, 69978 Israel. Current address: Mathematics Department, Technion, Haifa, 32000 Israel e-mail: iftahday@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that fractal percolation sets in 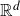$\mathbb{R}^{d}$ almost surely intersect every hyperplane absolutely winning (HAW) set with full Hausdorff dimension. In particular, if 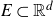$E\subset\mathbb{R}^{d}$ is a realisation of a fractal percolation process, then almost surely (conditioned on 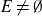$E\neq\emptyset$), for every countable collection 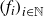$\left(f_{i}\right)_{i\in\mathbb{N}}$ of 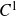$C^{1}$ diffeomorphisms of 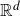$\mathbb{R}^{d}$, 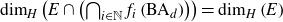$\dim_{H}\left(E\cap\left(\bigcap_{i\in\mathbb{N}}f_{i}\left(\text{BA}_{d}\right)\right)\right)=\dim_{H}\left(E\right)$, where 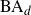$\text{BA}_{d}$ is the set of badly approximable vectors in 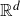$\mathbb{R}^{d}$. We show this by proving that E almost surely contains hyperplane diffuse subsets which are Ahlfors-regular with dimensions arbitrarily close to 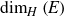$\dim_{H}\left(E\right)$.

We achieve this by analysing Galton–Watson trees and showing that they almost surely contain appropriate subtrees whose projections to 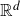$\mathbb{R}^{d}$ yield the aforementioned subsets of E. This method allows us to obtain a more general result by projecting the Galton–Watson trees against any similarity IFS whose attractor is not contained in a single affine hyperplane. Thus our general result relates to a broader class of random fractals than fractal percolation.

MSC classification

Primary: 28A80: Fractals 60J80: Branching processes (Galton-Watson, birth-and-death, etc.) 60D05: Geometric probability and stochastic geometry 11K60: Diophantine approximation
Secondary: 37C45: Dimension theory of dynamical systems 05C80: Random graphs
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 172 , Issue 3 , May 2022 , pp. 655 - 684
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

An, J., Guan, L. and Kleinbock, D.. Bounded orbits of diagonalisable flows on ${SL}_3(\mathbb {R})/{SL}_3(\mathbb {Z})$ . Internat. Math. Res. Notices, 2015. (24) (2015), 13623–13652.CrossRefGoogle Scholar
Broderick, R., Fishman, L. and Kleinbock, D.. Schmidt’s game, fractals, and orbits of toral endomorphisms. Ergodic Theory Dynam. Syst. 31(4) (2011), 1095–1107.CrossRefGoogle Scholar
Broderick, R., Fishman, L., Kleinbock, D., Reich, A. and Weiss, B.. The set of badly approximable vectors is strongly ${C}^1$ incompressible. Math. Proc. Camb. Phil. Soc. 153(2) (2012), 319–339.CrossRefGoogle Scholar
Broderick, R., Fishman, L. and Simmons, D.. Badly approximable systems of affine forms and incompressibility on fractals. J. Number Theory 133(7) (2013), 2186–2205.CrossRefGoogle Scholar
Bugeaud, Y.. Distribution Modulo One and Diophantine Approximation . Cambridge Tracts in Math. (Cambridge University Press, 2012).Google Scholar
Das, T., Fishman, L., Simmons, D. and UrbaŃski, M.. Badly approximable vectors and fractals defined by conformal dynamical systems. ArXiv e-prints, (Mar. 2016).Google Scholar
Dayan, Y.. Diophantine approximations on random fractals. arXiv e-prints, (Jul 2018).Google Scholar
Falconer, K. J.. Random fractals. Math. Proc. Camb. Phil. Soc. 100(3) (1986), 559–582.CrossRefGoogle Scholar
Falconer, K. J.. Fractal Geometry: Mathematical Foundations and Applications (Wiley, 2013).Google Scholar
Fishman, L., Kleinbock, D., Merrill, K. and Simmons, D.. Intrinsic diophantine approximation on manifolds: General theory. Trans. Amer Math. Soc. 370(1) (2018), 577–599.CrossRefGoogle Scholar
Hawkes, J.. Trees generated by a simple branching process. J. London Math. Soc. 24(2) (1981), 373–384.CrossRefGoogle Scholar
Hutchinson, J. E.. Fractals and self similarity. Indiana Univ. Math. J. 30(5) (1981), 713–747.CrossRefGoogle Scholar
Kesten, H. and Stigum, B. P.. A limit theorem for multidimensional Galton–watson processes. Ann. Math. Statistics. 37(5) (1966), 1211–1223.CrossRefGoogle Scholar
Kleinbock, D., Lindenstrauss, E. and Weiss, B.. On fractal measures and diophantine approximation. Selecta Math. 10(4) (2005), 479–523.CrossRefGoogle Scholar
Lyons, R. and Peres, Y.. Probability on Trees and Networks (Cambridge University Press, New York, 2016).CrossRefGoogle Scholar
Mauldin, R. D. and Williams, S. C.. Random recursive constructions: Asymptotic geometric and topological properties. Trans. Amer. Math. Soc. 295(1) (1986), 325–346.CrossRefGoogle Scholar
Moran, P. A. P.. Additive functions of intervals and hausdorff measure. Math. Proc. Camb. Phil. Soc. 42(1) (1946), 15–23.CrossRefGoogle Scholar
MÖrters, P. and Peres, Y.. Brownian Motion. Cambridge Series in Statistical and Probabilistic Mathematics (Cambridge University Press, 2010).Google Scholar
Nesharim, E. and Simmons, D.. Bad(s, t) is hyperplane absolute winning. Acta Arith. 164(2) (2014), 145–152.CrossRefGoogle Scholar
Pakes, A. and Dekking, F.. On family trees and subtrees of simple branching processes. J. Theoret. Probab. 4(2) (1991), 353–369.CrossRefGoogle Scholar
Schmidt, W. M.. On badly approximable numbers and certain games. Trans. Amer. Math. Soc. 123(1) (1966) 178–199, 1966.CrossRefGoogle Scholar