Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-14T22:06:36.219Z Has data issue: false hasContentIssue false
  • English
  • Français

Relative characters for H-projective RG-lattices

Published online by Cambridge University Press:  24 October 2008

Peter Symonds
Peter Symonds
Affiliation:
Ohio State University, Department of Mathematics, 231 West 18th Avenue, Columbus, Ohio 43210, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

If G is a group with a subgroup H and R is a Dedekind domain, then an H-projective RG-lattice is an RG-lattice that is a direct summand of an induced lattice 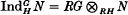for some RH-lattice N: they have been studied extensively in the context of modular representation theory. If H is the trivial group these are the projective lattices. We define a relative character χG/H on H-projective lattices, which in the case H = 1 is equivalent to the Hattori–Stallings trace for projective lattices (see [5, 8]), and in the case H = G is the ordinary character. These characters can be used to show that the R-ranks of certain H-projective lattices must be divisible by some specified number, generalizing some well-known results: cf. Corollary 3·6. If for example we take R = ℤ, then |G/H| divides the ℤ-rank of any H-projective ℤG-lattice.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 104 , Issue 2 , September 1988 , pp. 207 - 213
Copyright
Copyright © Cambridge Philosophical Society 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Berman, S. D.. Integral representations of finite groups. Dokl. Akad. Nauk. SSSR 106 (1956), 1286–1287Google Scholar
English translation Soviet Math. Dokl. 4 (1963), 1533–1535.Google Scholar
[2]Curtis, C. W. and Reiner, I.. Methods of Representation Theory – with Applications to Finite Groups and Orders, vol. 1 (Wiley, 1981).Google Scholar
[3]Dress, A.. On the Krull–Schmidt theorem for integral group representations of rank 1. Michigan Math. J. 17 (1970), 273–277.CrossRefGoogle Scholar
[4]Green, J. A.. On the indecomposable representations of a finite group. Math. Z. 70 (1959), 430–445.CrossRefGoogle Scholar
[5]Hattori, A.. Rank element of a projective module. Nagoya Math. J. 25 (1965), 113–120.CrossRefGoogle Scholar
[6]Higman, D. G.. Indecomposable representations at characteristic p. Duke Math. J. 21 (1954), 377–381.CrossRefGoogle Scholar
[7]Lee, M. P.. Integral representations of dihedral groups of order 2p. Trans. Amer. Math. Soc. 110 (1964), 213–231.Google Scholar
[8]Stallings, J. R.. Centerless groups – an algebraic formulation of Gottlieb's theorem. Topology 4 (1965), 129–134.CrossRefGoogle Scholar
[9]Swan, R. G.. Induced representations and projective modules. Ann. of Math. 71 (1960), 552–578.CrossRefGoogle Scholar