Hostname: page-component-5447f9dfdb-6cxwp Total loading time: 0 Render date: 2025-07-28T20:46:27.967Z Has data issue: false hasContentIssue false
  • English
  • Français

Relativistic wave equations for zero rest-mass

Published online by Cambridge University Press:  24 October 2008

Lars Gårding
Lars Gårding
Affiliation:
The Institute of Mathematics of the University of Lund, Sweden, and Wesley House, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

1. In this paper I establish in a certain sense all the relativistically invariant sets of linear partial homogeneous differential equations in which every unknown function u satisfies 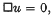being the relativistic Laplace operator. Analogous questions for any orthogonal group are dealt with in a previous paper, but it was thought that an independent and not too technical treatment for the Lorentz group might be of interest.

Information

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 41 , Issue 1 , June 1945 , pp. 49 - 56
Copyright
Copyright © Cambridge Philosophical Society 1945

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

1Brauer, R. and Weyl, H.Spinors in n dimensions. American J. Math. 57 (1935), 425.CrossRefGoogle Scholar
2Cartan, E.La théorie des spineurs. I, II. Act. Scient. 643, 701 (1936).Google Scholar
3Dirac, P. A. M.Relativistic wave equations. Proc. Roy. Soc. A, 155 (1936), 447.Google Scholar
4Gårding, L. On a class of linear transformations connected with group representations. Diss., Lund (1944).Google Scholar
5Van Der Waerden, B. L.Nachr. Ges. Wiss. Gött. (1929), 100.Google Scholar