No CrossRef data available.
A remark on the K-theory of BГq
Published online by Cambridge University Press: 24 October 2008
Extract
1. In (4) Bott and Heitsch discussed certain classifying spaces of importance in the study of foliations of various types. For example they studied the space BГq which helps to classify real foliations of codimension q and proved that a canonical map
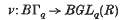
induces an injection in integral cohomology for q ≥ 2. Similar results hold for classifying spaces BUГq and BSГq related to complex and oriented foliations respectively. The object of this paper is to demonstrate that the canonical maps referred to above also induce injections in integral K-theory.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 78 , Issue 2 , September 1975 , pp. 309 - 314
- Copyright
- Copyright © Cambridge Philosophical Society 1975


