Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-26T06:28:20.306Z Has data issue: false hasContentIssue false
  • English
  • Français

Rigidity in dimension four of area-minimising Einstein manifolds

Published online by Cambridge University Press:  23 January 2015

A. BARROS ,
C. CRUZ ,
R. BATISTA  and
P. SOUSA
A. BARROS
Affiliation:
Department of Mathematics, Universidade Federal do Ceará, 60455-760 - Fortaleza-CE, Brazil. e-mail: abbarros@mat.ufc.br, tiarlos@mat.ufc.br
C. CRUZ
Affiliation:
Department of Mathematics, Universidade Federal do Ceará, 60455-760 - Fortaleza-CE, Brazil. e-mail: abbarros@mat.ufc.br, tiarlos@mat.ufc.br
R. BATISTA
Affiliation:
Department of Mathematics, Universidade Federal do Piauí, 64049-550 - Teresina-PI, Brazil. e-mail: marcolino@ufpi.edu.br, e-mail: paulosousa@ufpi.edu.br
P. SOUSA
Affiliation:
Department of Mathematics, Universidade Federal do Piauí, 64049-550 - Teresina-PI, Brazil. e-mail: marcolino@ufpi.edu.br, e-mail: paulosousa@ufpi.edu.br
Get access Rights & Permissions [Opens in a new window]

Abstract

The aim of this paper is to prove a sharp inequality for the area of a four dimensional compact Einstein manifold (Σ, gΣ) embedded into a complete five dimensional manifold (M5, g) with positive scalar curvature R and nonnegative Ricci curvature. Under a suitable choice, we have 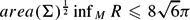$area(\Sigma)^{\frac{1}{2}}\inf_{M}R \leq 8\sqrt{6}\pi$. Moreover, occurring equality we deduce that (Σ, gΣ) is isometric to a standard sphere (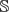$\mathbb{S}$4, gcan) and in a neighbourhood of Σ, (M5, g) splits as ((-ϵ, ϵ) × 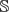$\mathbb{S}$4, dt2 + gcan) and the Riemannian covering of (M5, g) is isometric to $\Bbb{R}$ × 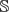$\mathbb{S}$4.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 158 , Issue 2 , March 2015 , pp. 355 - 363
Copyright
Copyright © Cambridge Philosophical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Anderson, M. T.On Area-Minimising hypersurfaces in manifolds of non-negative curvature. Indiana Univ. Math. J. 32 (1983), 745–760.Google Scholar
[2]Avez, A.Application de la formule de Gauss–Bonnet–Chern aux variétés à quatre dimensions. C.R.A.S. 256 (1963), 5488–5490.Google Scholar
[3]Bray, H., Brendle, S. and Neves, A.Rigidity of area-minimising two-spheres in three-manifolds. Comm. Anal. Geom. 18 (2010), 821–830.Google Scholar
[4]Bray, H., Brendle, S., Eichmair, M. and Neves, A.Area-minimising projective planes in three-manifolds. Comm. Pure. Appl. Math. 63 (1980), 1237–1247.Google Scholar
[5]Berger, M.Sur les variétés d'Einstein compactes. C. R. de la III^ Réunion du Groupemnt des Mathématiques D'expression Latine (Namur, 1965), pp. 35–55.Google Scholar
[6]Bombieri, E. and de Giorgi, E.Minimal cones and the Bernstein problem. Invent. Math. 7 (1968), 243–269.Google Scholar
[7]Cai, M. and Galloway, G.Rigidity of area minimising tori in 3-manifolds of nonnegative scalar curvature. Comm. Anal. Geom. 8 (2000), 565–573.Google Scholar
[8]Cheeger, J. and Ebin, D.Comparison Theorems in Riemannian Geometry. vol 365. (American Mathematical Society, Chelsea Publishing, Providence, RI, 2008), 161 pp.Google Scholar
[9]Cheeger, J. and Gromoll, D.The splitting theorem for manifolds of non-negative Ricci curvature. J. Differential Geom. 6 (1971), 119–128.Google Scholar
[10]Gursky, M. J.Locally conformally flat four and six-manifolds of positive scalar curvature and positive Euler characteristic. Indiana Univ. Math. J. 43 (1994), 747–774.Google Scholar
[11]Huisken, G. and Ilmanen, T.The inverse mean curvature flow and the Riemannian Penrose inequality. J. Differential Geom. 59 (2001), 353–437.CrossRefGoogle Scholar
[12]Huisken, G. and Yau, S.T.Deffinition of center of mass for isolated physical systems and unique foliations by stable spheres with constant mean curvature. Invent. Math. 124 (1996), 281–311.CrossRefGoogle Scholar
[13]Leite, M. L.Rotational hypersurfaces of space forms with constant scalar curvature. Manuscripta Math. 67 (1990), 285–304.Google Scholar
[14]Mazzeo, R., Pollack, D. and Uhlenbeck, K.Moduli spaces of singular Yamabe metrics. J. Amer. Math. Soc. 9 (1996), 303–344.Google Scholar
[15]Micallef, M. and Moraru, V. Splitting of 3-manifolds and rigidity of area-minimising surfaces, arXiv:1107.5346.Google Scholar
[16]Nabonnand, P.Sur les variétés Riemanniennes complètes à courbure de Ricci positive. C.R. Acad. Sci. Paris. 291 (1980), 591–593.Google Scholar
[17]Nunes, I. Rigidity of Area-Minimising hyperbolic surfaces in three-manifolds. PhD. thesis. IMPA (2011).Google Scholar
[18]Nunes, I.Rigidity of Area-Minimising hyperbolic surfaces in three-manifolds. J. Geom. Anal. 23 (2013), 1290–1302.Google Scholar
[19]Seshadri, H.Weyl curvature and the Euler characteristic in dimension four. Differential Geom. App. 24 (2006), 172–177.Google Scholar
[20]Schoen, R.Variational theory for the total scalar curvature funcional for Riemannian metrics and related topics, Topics in calculus of variations (Montecatini Terme, 1987), Lecture Notes in Math. vol. 1365 (Springer-Verlag, 1989), pp. 120–154.Google Scholar
[21]Schoen, R.Conformal deformation of a Riemannian metric to constant scalar curvature. J. Differential Geom. 20 (1984), 479–495.Google Scholar
[22]Santos, A.A construction of constant scalar curvature manifolds with Delaunay-type ends. Ann. Henri Poincaré. 10 (2010), 1487–1535.CrossRefGoogle Scholar
[23]Toponogov, V.Evaluation of the length of a closed geodesic on a convex surface. Dokl. Akad. Nauk. SSSR. 124 (1959), 282–284.Google Scholar