Published online by Cambridge University Press: 24 October 2008
Let E[τ] be a locally convex Hausdorif topological vector space, with a Schauder basis {xi, x′j where
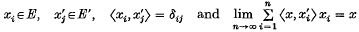
for each x ∈ E. The partial summation operator Sn, defined by
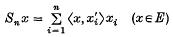
is a linear operator on E, whose definition extends at once to a linear operator mapping (E′)* into E, where (E′)* is the algebraic dual of E′. The dual of Sn is the operator S′n, mapping E* into E′, defined by
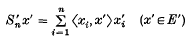
and 〈Snx, x′〉 = 〈x, S′nx′〉 for each x ∈ (E′)*. It is easy to see that S′nx′ → x′ with respect to the weak topology σ(E′, E) for each x′ ∈ E′.