Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-26T18:24:56.006Z Has data issue: false hasContentIssue false
  • English
  • Français

Sets of zero discrete harmonic density

Published online by Cambridge University Press:  20 November 2009

COLIN C. GRAHAM  and
KATHRYN E. HARE
COLIN C. GRAHAM
Affiliation:
Department of Mathematics, University of British Columbia, V6T 1Y4 Vancouver, B.C., Canada. e-mail: ccgraham@alum.mit.edu
KATHRYN E. HARE
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, Ontario N2L 3G1 Canada. e-mail: kehare@uwaterloo.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a compact, connected, abelian group with dual group Γ. The set E ⊂ 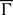has zero discrete harmonic density (z.d.h.d.) if for every open U ⊂ G and μ ∈ Md(G) there exists ν ∈ Md(U) with 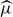= 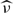on E. I0 sets in the duals of these groups have z.d.h.d. We give properties of such sets, exhibit non-Sidon sets having z.d.h.d., and prove union theorems. In particular, we prove that unions of I0 sets have z.d.h.d. and provide a new approach to two long-standing problems involving Sidon sets.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 148 , Issue 2 , March 2010 , pp. 253 - 266
Copyright
Copyright © Cambridge Philosophical Society 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bourgain, J. Subspaces of l ∞N, arithmetical diameter and Sidon sets. in Probability in Banach spaces, V (Medford, Mass., 1984), 96–127. Lecture Notes in Math. 1153 (Springer, Berlin, 1985).Google Scholar
[2]Déchamps–Gondim, M.Ensembles de Sidon topologiques. Ann. Inst. Fourier (Grenoble) 22, fasc.3 (1972).CrossRefGoogle Scholar
[3]Déchamps, M. and Selles, O.Compacts associés aux sommes de suites lacunaires. Publ. Math. Orsay 01 (1996) 27–40Google Scholar
[4]Gaposhkin, V. F.A uniqueness theorem for multiple lacunary trigonometric series. Mat. Zametki 16 (1974) 865–870 (Translated in Math. Notes 16 (1974) 1112–1115)Google Scholar
[5]Graham, C. C. and Hare, K. E.ϵ-Kronecker and I 0 sets in abelian groups, I: arithmetic properties of ϵ-Kronecker sets. Math. Proc. Camb. Phil. Soc. 140 (2006), no. 3, 475–489.CrossRefGoogle Scholar
[6]Graham, C. C. and Hare, K. E.ϵ-Kronecker and I 0 sets in abelian groups, III: Interpolation by measures on small sets, Studia Math. 171 (2005), no. 1, 15–32.CrossRefGoogle Scholar
[7]Graham, C. C., Hare, K. E. and Ramsey, L. T.Union problems for I 0 sets. Acta Sci. Math. (Szeged) 75 (2009), 175–195.Google Scholar
[8]Graham, C. C. and McGehee, O. CarruthEssays in Commutative Harmonic Analysis. (Springer-Verlag 1979).CrossRefGoogle Scholar
[9]Hadamard, J.Essai sur l'étude des fonctions données par leur développement de Taylor. J. Math. Pures Appl. (4) 8 (1892) 101–186Google Scholar
[10]Kahane, J.-P. and Katznelson, Y.Entiers aléatoires et analyse harmonique. J. Anal. Math. 105 (2008), 363–378.CrossRefGoogle Scholar
[11]Kalton, J. N.On Vector-valued inequalities for Sidon sets and sets of interpolation. Colloq. Math. 54 (1993) 233–244CrossRefGoogle Scholar
[12]Lopez, J. and Ross, K.Sidon sets. Lecture Notes in Pure and Applied Math. 13 (Marcel Dekker 1975).Google Scholar
[13]Méla, J.-F.Approximation diophantine et ensembles lacunaires. Mem. Bull. Math. Soc. France 19 (1969) 26–54Google Scholar
[14]Ramsey, L. T.A theorem of C. Ryll-Nardzewski and metrizable l.c.a. groups. Proc. Amer. Math. Soc. 78 (1980) no. 2, 221–224CrossRefGoogle Scholar
[15]Rudin, W.Fourier Analysis on Groups. (Wiley Interscience 1962).Google Scholar
[16]Ryll-Nardzewski, C.Concerning almost periodic extensions of functions. Colloq. Math. 12 (1964) 235–237CrossRefGoogle Scholar
[17]Shapiro, G. S.Balayage in Fourier transforms: general results, perturbation, and balayage with sparse frequencies. Trans. Amer. Math. Soc. 225 (1977), 183–198.CrossRefGoogle Scholar
[18]Shapiro, G. S.Unique balayage in Fourier transforms on compact abelian groups. Proc. Amer. Math. Soc. 70 (1978), no. 2, 146–150.CrossRefGoogle Scholar
[19]Zygmund, A.On a theorem of Hadamard. Ann. Soc. Polon. Math. 21 (1948) 52–69Google Scholar