No CrossRef data available.
Simple reduction theorems for extension and torsion functors
Published online by Cambridge University Press: 24 October 2008
Extract
Let Λ be a commutative ring with an identity element and c an element of Λ which is not a zero divisor Denote by Ω the residue class ring Λ/Λc. If now M is a Λ-module for which c is not a zero divisor, and A is an Ω-module, then a theorem of Rees (2) asserts that, for every non-negative integer n, we have a Λ-isomorphism
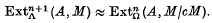
This reduction theorem has found a number of useful and interesting applications.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 57 , Issue 3 , July 1961 , pp. 483 - 488
- Copyright
- Copyright © Cambridge Philosophical Society 1961
References
REFERENCES
(2)Rees, D.A theorem of homological algebra. Proc. Camb. Phil. Soc. 52 (1956), 605–10.CrossRefGoogle Scholar


