Published online by Cambridge University Press: 24 October 2008
The purpose of this article is to derive a set of ‘easily verifiable’ sufficient conditions for the asymptotic stability of the trivial solution of a class of linear neutral integro-delay-differential equations of the form
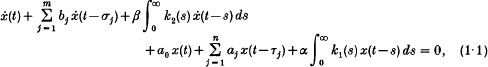
where ẋ denotes the right derivative, and then generalize the result to a vector system. Asymptotic stability of the trivial solution of the form (1·1) and several of its variants has been considered by many authors (see the discussion at the end). Also, there exists a well developed fundamental theory for neutral delay-differential equations (e.g. existence, uniqueness, continuous dependence etc. of solutions; see for instance the survey article by Akhmerov[1] and the references in it); however there exists no ‘easily verifiable’ sufficient condition for the asymptotic stability of the trivial solution of (1·1). By the term ‘easily verifiable’ we mean a verification which is as easy as in the case of Routh-Hurwitz criterion or the diagonal dominance condition of a matrix. A number of results which are valid for linear autonomous ordinary and delay-differential equations cannot be generalized (or extended) to neutral equations. It has been shown by Gromova and Zverkin [8] that a linear neutral differential equation can have unbounded solutions even though the related characteristic equation has only purely imaginary roots (see also Gromova[7], Datko[3], Snow [16], Brumley [2]); such behaviour is not possible in the case of ordinary or (non-neutral) delay-differential equations. It is known (theorem 6·1 of Henry [10]) that if the characteristic equation associated with a only with negative real parts and if all the roots are uniformly bounded away from the imaginary axis, then asymptotic stability of the trivial solution can be asserted.