Singular n-tuples and Hausdorff dimension
Published online by Cambridge University Press: 24 October 2008
Extract
1. Introduction. Throughout the paper θ = (θ1, …, θn), φ = (φ1, …, φn), … denote points of Euclidean space Rn. We write Kn for the set of θ in Rn for which θl, …, θn, 1 are linearly independent over the rational numbers. We denote points of the set of integer n-tuples Zn by x, y, … We write
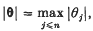
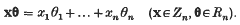
If α is a real number, ∥α∥ denotes the distance from α to the nearest integer.
Let θ ∈ Rn. By a theorem of Dirichlet ((2), chapter 1, theorem VI).
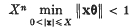
for all X ≥ 1. We say that θ is singular if
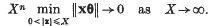
Singular points form a set of n-dimensional Lebesgue measure zero. In fact, H. Davenport and W. M. Schmidt (3) showed that
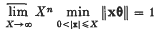
for almost all θ in Rn. Although there are no singular numbers in Kl ((2), p. 94) there are ‘highly singular’ n-tuples in Kn for n ≥ 2.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 81 , Issue 3 , May 1977 , pp. 377 - 385
- Copyright
- Copyright © Cambridge Philosophical Society 1977
References
REFERENCES
- 11
- Cited by


