No CrossRef data available.
≡ 0 (mod p)
Published online by Cambridge University Press: 24 October 2008
Throughout this paper a0, a1, a2, l1, l2 denote fixed integers with l1 ≥ 2, l2 ≥ 2. We let l = max(l1, l2) and let P be the set of primes 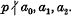 Mordell (4) has shown that for any sufficiently large prime p the congruence
Mordell (4) has shown that for any sufficiently large prime p the congruence
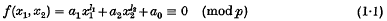
is soluble. Thus there are at most a finite number of such p for which (1·1) is insoluble. If there is at least one prime p ∈ P for which (1·1) is insoluble, we let p0 denote the largest of such p, so that (1·1) is soluble for all p ∈ P with p > p0 but not for p = p0. Otherwise (1·1) is soluble for p ∈ P and we let p0 = 1. From the work of Mordell (4) we have

For p ∈ P with p > p0 (1·1) is thus always soluble and any such solution (x1, x2) can be taken to satisfy

Chalk(2) has posed the problem of estimating a ‘small’ solution of (1·1), at least for p sufficiently large; that is a solution for which p in the inequality (1·3) can be replaced by something less than p. Smith(5) has shown that for p sufficiently large there is always a solution satisfying 1 ≤ xi ≪ p¾log p (i = 1, 2). It is the purpose of this paper to prove the following sharper and more precise result.