No CrossRef data available.
Some canonical triple surfaces
Published online by Cambridge University Press: 24 October 2008
Extract
1. In 1891, Castelnuovo suggested that there may exist canonical surfaces which consist of three sheets covering the same surface. In particular, he remarked that, if the canonical curves of a surface contain a 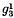 then the canonical model of the surface is certainly a three-sheeted surface. An example is the quintic surface with a tacnode, in space of three dimensions; its canonical model is a triple plane, branching along a curve of order 12 with twenty-four cusps which lie on a quartic.
then the canonical model of the surface is certainly a three-sheeted surface. An example is the quintic surface with a tacnode, in space of three dimensions; its canonical model is a triple plane, branching along a curve of order 12 with twenty-four cusps which lie on a quartic.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 32 , Issue 3 , October 1936 , pp. 366 - 372
- Copyright
- Copyright © Cambridge Philosophical Society 1936
References
* Castelnuovo, G., Rend. Ist. Lomb. (2), 24 (1891), 307–18.Google Scholar
† Enriques, F., Lezioni sulla teoria delle superficie algebriche, Padova, 1930, § 56, p. 347.Google Scholar
‡ Babbage, D. W., Proc. Camb. Phil. Soc. 30 (1934), 297–308.CrossRefGoogle Scholar
§ Dr Babbage adds the following note: “If the general canonical curve of a surface contains a ![]() its canonical model is a surface of three sheets superimposed on a plane, a rational normal scroll, or a Veronese surface. The remark in my paper was based on the theorem that a curve on a surface is met in a set of points equivalent to a canonical set minus a characteristic set by a curve of the canonical system augmented by the exceptional curves. For the hypothetical canonical triple surfaces considered there can in general be no exceptional curves, for such a curve must impose only one condition on a prime to contain it; the argument in this case is correct. But in the case of a triple cone the neighbourhood of the vertex has to be considered as an infinitesimal curve, and it may happen that this curve, or part of it if it is reducible, is exceptional in the Noether sense: it is this possibility which was overlooked by me and is illustrated by Dr Bronowski's examples.”
its canonical model is a surface of three sheets superimposed on a plane, a rational normal scroll, or a Veronese surface. The remark in my paper was based on the theorem that a curve on a surface is met in a set of points equivalent to a canonical set minus a characteristic set by a curve of the canonical system augmented by the exceptional curves. For the hypothetical canonical triple surfaces considered there can in general be no exceptional curves, for such a curve must impose only one condition on a prime to contain it; the argument in this case is correct. But in the case of a triple cone the neighbourhood of the vertex has to be considered as an infinitesimal curve, and it may happen that this curve, or part of it if it is reducible, is exceptional in the Noether sense: it is this possibility which was overlooked by me and is illustrated by Dr Bronowski's examples.”
* If n has its least value three, this type of surface has as canonical model (a particular case of) the known triple plane mentioned in § 1.


