Published online by Cambridge University Press: 24 October 2008
1. The purpose of this paper is to examine in detail the types of radiation emitted by a quantum mechanical system (representing a nucleus) when the radiating particle changes its azimuthal quantum number l by two, one, or nought. We assume that the radiating particle is spinless* and that it moves in a field possessing central symmetry, so that the particle may be described by a wave function ψn,l,m which factorizes into radial and angular parts,
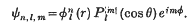
We assume secondly that the nucleus has a finite radius aN of the order of 10−12 cm., that is to say that π(r) = 0 for r > aN.
page 407 note ** The case of a radiating particle with spin has also been investigated, and it will be shown shortly that it yields different results which have an important bearing on the theory of internal conversion of γ rays.
page 407 note † Taylor, H. M. and Mott, N. F., Proc. Roy. Soc. A, 138 (1932), 666Google Scholar. This paper will be referred to as TM.
page 407 note ‡ Hulme, H. R., Proc. Roy. Soc. A, 138 (1932). 643.CrossRefGoogle Scholar
page 409 note * Cf. equations (4.44) and (4.46).
page 412 note * It should perhaps be mentioned that the sign of π in the potentials (3.06) and (3.08) is positive or negative according as Δm is positive or negative in (3.05) and (3.07). This difference is, however, quite trivial, and we consider only the positive sign.
page 412 note † Cf. Frenkel, J., Elektrodynamik, p. 94, Berlin (1926).Google Scholar