Some Theorems on Abelian Integrals Associated with an Algebraic Variety
Published online by Cambridge University Press: 24 October 2008
Extract
1. In some recent papers I have developed the theory of what I have called harmonic integrals associated with an algebraic variety. My object has been to provide an apparatus with which to investigate the properties of the classical integrals
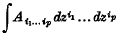
of total differentials which are finite everywhere on an algebraic variety Vm of m dimensions
These integrals are referred to in what follows as “Abelian integrals”, as it is desirable to have a single name to denote all integrals of this type. The usual qualification “of the first kind” is omitted, and is always to be understood. In the present paper it is shown how the theory of harmonic integrals can be applied to deduce certain results concerning Abelian integrals, and a number of interesting problems are suggested by these results.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 31 , Issue 1 , January 1935 , pp. 18 - 25
- Copyright
- Copyright © Cambridge Philosophical Society 1935
References
* Proc. London Math. Soc. (2), 38 (1934), 72–95Google Scholar and in the press. Also Journal London Math. Soc. 8 (1933), 312–19Google Scholar. These papers will be referred to as I, II, and III respectively.
† Lefschetz, S., L'Analyse Situset la Géométric Algébrique (Gauthier-Villars, 1924), chap. v.Google Scholar
* Veblen, O., Trans. American Math. Soc. 25 (1923), 540–50.CrossRefGoogle Scholar
* Lefschetz, loc. cit. p. 105.
* Journal London Math. Soc. 5 (1930), 283–90.Google Scholar
† Lefschetz, loc. cit. p. 103. The restriction to m = 3 is not essential.
- 3
- Cited by

