Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-02-03T23:38:53.109Z Has data issue: false hasContentIssue false
  • English
  • Français

Some unexpectedly non-singular orbit spaces

Published online by Cambridge University Press:  24 October 2008

H. R. Morton
H. R. Morton
Affiliation:
University of Liverpool
Get access Rights & Permissions [Opens in a new window]

Extract

The orbit space of a manifold under the smooth action of a compact Lie group is typically a ‘manifold with singularities’. The orbits of a given type each form a mani-fold, but these ‘strata’ generally do not give a manifold when pieced together. For example, the orbit space of S3 under the action of 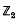given by the matrix.

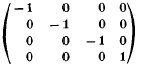
is the suspension of 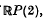P(2), which fails to be a manifold at the suspension points.

In this paper I shall give examples where, in spite of having many orbit types, the orbit space is a manifold, with or without boundary.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 82 , Issue 1 , July 1977 , pp. 35 - 37
Copyright
Copyright © Cambridge Philosophical Society 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Hsiang, W.-C. and Hsiang, W.-Y.Differentiable actions of compact classical groups. I. Amer. J. Math. 89 (1967), 705–786.CrossRefGoogle Scholar
(2)Spanier, E. H.Algebraic Topology (McGraw-Hill, 1966).Google Scholar