Stable cohomotopy and cobordism of abelian groups
Published online by Cambridge University Press: 24 October 2008
Extract
The object of this paper is to prove that for a finite abelian group G the natural map 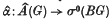 is injective, where Â(G) is the completion of the Burnside ring of G and σ0(BG) is the stable cohomotopy of the classifying space BG of G. The map â is detected by means of an M U* exponential characteristic class for permutation representations constructed in (11). The result is a generalization of a theorem of Laitinen (4) which treats elementary abelian groups using ordinary cohomology. One interesting feature of the present proof is that it makes explicit use of the universality of the formal group law of M U*. It also involves a computation of M U*(BG) in terms of the formal group law. This may be of independent interest. Since writing the paper the author has discovered that M U*(BG) has previously been calculated by Land-weber(5).
is injective, where Â(G) is the completion of the Burnside ring of G and σ0(BG) is the stable cohomotopy of the classifying space BG of G. The map â is detected by means of an M U* exponential characteristic class for permutation representations constructed in (11). The result is a generalization of a theorem of Laitinen (4) which treats elementary abelian groups using ordinary cohomology. One interesting feature of the present proof is that it makes explicit use of the universality of the formal group law of M U*. It also involves a computation of M U*(BG) in terms of the formal group law. This may be of independent interest. Since writing the paper the author has discovered that M U*(BG) has previously been calculated by Land-weber(5).
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 90 , Issue 2 , September 1981 , pp. 273 - 278
- Copyright
- Copyright © Cambridge Philosophical Society 1981
References
REFERENCES
- 5
- Cited by


