Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-14T22:14:09.149Z Has data issue: false hasContentIssue false
  • English
  • Français

Subrings of the first neighbourhood ring: II

Published online by Cambridge University Press:  24 October 2008

D. Kirby
D. Kirby
Affiliation:
University of Southampton
Get access Rights & Permissions [Opens in a new window]

Extract

In (1) and (2) we studied a lattice 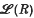of extension rings associated with a commutative ring R with identity. When R, M is a one-dimensional Cohen-Macaulay local ring the elements of 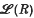are just those integral extensions of R contained in the total quotient ring T(R) and such that lengthR(S/R) is finite. Experiments with local rings of singular points on algebraic curves indicate that only the simplest singularities give rise to finite lattices. So the problem arises as to which local rings R give rise to which finite lattices. In later papers this problem will be investigated in detail, at least when R is of low embedding dimension. The purpose of the present note is to establish some general results which indicate the size of the problem.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 92 , Issue 1 , July 1982 , pp. 35 - 39
Copyright
Copyright © Cambridge Philosophical Society 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Kirby, D.Subrings of the first neighbourhood ring. Math. Proc. Cambridge Phil. Soc. 86 (1979), 205–214.CrossRefGoogle Scholar
(2)Kirby, D. and Adranghi, M. R.A lattice of extension rings for a commutative ring. Math. Proc. Cambridge Phil. Soc. 84 (1978), 225–234.CrossRefGoogle Scholar
(3)Matlis, E.The multiplicity and reduction number of a one-dimensional local ring. Proc. London Math. Soc. 26 (1973), 273–288.CrossRefGoogle Scholar
(4)Northcott, D. G.The neighbourhoods of a local ring. J. London Math. Soc. 30 (1955), 360–375.CrossRefGoogle Scholar
(5)Northcott, D. G.A general theory of one-dimensional local rings. Proc. Glasgow Math. Soc. 2 (1956), 159–169.CrossRefGoogle Scholar
(6)Northcott, D. G.Lessons on rings, modules and multiplicities (Cambridge University Press, 1968).CrossRefGoogle Scholar