The sum of powers as canonical expression
Published online by Cambridge University Press: 24 October 2008
Extract
1. In this paper I discuss the expression of the general form F of order n, homogeneous in r + 1 variables z0, z1,…, zl,…, zr, as the sum of the nth powers of h + H linear forms in these variables. I take h (> 0) of these linear forms to be undetermined, namely the forms
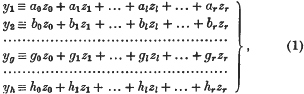
whose coefficients are undetermined; and I take the remaining H(≥0) linear forms to be assigned, namely the forms

whose coefficients are assigned.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 29 , Issue 1 , January 1933 , pp. 69 - 82
- Copyright
- Copyright © Cambridge Philosophical Society 1933
References
* This corollary, sometimes ascribed to Wakeford, E. K., Proc. London Math. Soc. (2), 18 (1919), 403,Google Scholar was given by Lasker, Em., Math. Annalen, 58 (1904), 434CrossRefGoogle Scholar, whose paper substantially anticipates that of E. K. Wakeford. It can be proved geometrically by applying to the manifold ![]() of § 10 the theorem of Terracini, A., Rend. di Palermo, 31 (1911), 392.CrossRefGoogle Scholar
of § 10 the theorem of Terracini, A., Rend. di Palermo, 31 (1911), 392.CrossRefGoogle Scholar
* Bertini, E., Rend. Lincei (5), 10 (1901), 73Google Scholar or Geometria proiettiva degli iperspazi, 2nd edn. (1923), 277. For a proof of the theorem without the aid of this lemma, see § 8.
* See for example Palatini, F., Rend. Lincei (5), 12 (1903), 378Google Scholar, and Atti Acc. Torino, 38 (1902), 43.Google Scholar
* Palatini, F., Atti Acc. Torino, 41 (1905–1906), 634.Google Scholar
* So for the general manifolds ![]() in space of 2r + 1 dimensions, a unique chord of which passes through a general point of the containing space. See Edge, W. L., Proc. Camb. Phil. Soc. 28 (1932), 285CrossRefGoogle Scholar. I remark here that a consequence of Theorem 3 is: it is a necessary condition, in order that through a general point of N pass two (h − 1)-dimensional spaces each containing h points of M′r, that the grade of the system S is equal to 2. So the surface V 62 in 5-dimensional space (given by W. L. Edge) has two apparent double points; it is rational, and its representative system is therefore one which the addition of a further base-node reduces to a system of grade 2—being, in fact, the system of plane quartics with a base-node and 6 simple base-points.
in space of 2r + 1 dimensions, a unique chord of which passes through a general point of the containing space. See Edge, W. L., Proc. Camb. Phil. Soc. 28 (1932), 285CrossRefGoogle Scholar. I remark here that a consequence of Theorem 3 is: it is a necessary condition, in order that through a general point of N pass two (h − 1)-dimensional spaces each containing h points of M′r, that the grade of the system S is equal to 2. So the surface V 62 in 5-dimensional space (given by W. L. Edge) has two apparent double points; it is rational, and its representative system is therefore one which the addition of a further base-node reduces to a system of grade 2—being, in fact, the system of plane quartics with a base-node and 6 simple base-points.
* Severi, F., Rend. di Palermo, 15 (1901), 33.CrossRefGoogle Scholar
- 15
- Cited by


