Summability methods which include the Riesz typical means. I
Published online by Cambridge University Press: 24 October 2008
Extract
A number of special results exist for summability methods B which, include Riesz summability (R,λ,k)—for example, when B is generalized Abel summability (A,λ,ρ) [Kuttner(5)], or Riemann summability (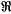 ,λ,μ) [Russell(14)], or Riemann-Cesàro summability (
,λ,μ) [Russell(14)], or Riemann-Cesàro summability (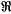 ,λ,p,α) [Rangachari(12)], or generalized Cesàro summability (C,λ,k) [Meir (9); Borwein and Russell (l)]. The question of necessary and sufficient conditions to be satisfied by an arbitrary method B in order that B ⊇ (R,λ,k) has received an answer only for limited values of λ and k—for example, by Lorentz [(6), Theorem 10] for k = 1; the restrictions on λ in this case were removed by Maddox [(8), Theorem 1]. Thus (apart from the well-known case k = 0) the case k = 1 is the only one for which a complete solution exists, though application of a theorem of Russell [(13), Theorem 1A] yields one form of a result for 0 < k ≤ 1. Maddox's results, however, suggest an alternative form capable of generalization to all k ≥ 0, and in this paper we obtain a complete solution for 0 < k ≤ 1 in that form, without restriction on λ. We first recall the following definitions.
,λ,p,α) [Rangachari(12)], or generalized Cesàro summability (C,λ,k) [Meir (9); Borwein and Russell (l)]. The question of necessary and sufficient conditions to be satisfied by an arbitrary method B in order that B ⊇ (R,λ,k) has received an answer only for limited values of λ and k—for example, by Lorentz [(6), Theorem 10] for k = 1; the restrictions on λ in this case were removed by Maddox [(8), Theorem 1]. Thus (apart from the well-known case k = 0) the case k = 1 is the only one for which a complete solution exists, though application of a theorem of Russell [(13), Theorem 1A] yields one form of a result for 0 < k ≤ 1. Maddox's results, however, suggest an alternative form capable of generalization to all k ≥ 0, and in this paper we obtain a complete solution for 0 < k ≤ 1 in that form, without restriction on λ. We first recall the following definitions.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 69 , Issue 1 , January 1971 , pp. 99 - 106
- Copyright
- Copyright © Cambridge Philosophical Society 1971
References
REFERENCES
- 4
- Cited by


