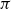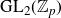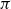1. Introduction
It is a classical problem in analysis and mathematical physics, more precisely Quantum Chaos, to bound the
![]() $L^{\infty}$
-norm of certain eigenfunctions on manifolds. In the most basic situation one considers a Riemann surfaces X of finite volume and eigenfunctions
$L^{\infty}$
-norm of certain eigenfunctions on manifolds. In the most basic situation one considers a Riemann surfaces X of finite volume and eigenfunctions
![]() $\phi$
of the Laplace–Beltrami operator
$\phi$
of the Laplace–Beltrami operator
![]() $\Delta_X$
. A sup-norm bound in the spectral aspect is then an estimates of the form
$\Delta_X$
. A sup-norm bound in the spectral aspect is then an estimates of the form
where
![]() $\lambda_{\phi}={1}/{4}+t_{\phi}^2$
is the Laplace–Beltrami eigenvalue of
$\lambda_{\phi}={1}/{4}+t_{\phi}^2$
is the Laplace–Beltrami eigenvalue of
![]() $\phi$
. The local bound corresponds to
$\phi$
. The local bound corresponds to
![]() $\delta=0$
and is known in great generality. The sup-norm problem asks for improved bounds featuring some
$\delta=0$
and is known in great generality. The sup-norm problem asks for improved bounds featuring some
![]() $\delta>0$
. The sup-norm problem has only been solved for very special surfaces X and is hopeless in general. Indeed there is a well-known obstruction to the sup-norm problem coming from large eigenspaces
$\delta>0$
. The sup-norm problem has only been solved for very special surfaces X and is hopeless in general. Indeed there is a well-known obstruction to the sup-norm problem coming from large eigenspaces
![]() $V_{\lambda}$
given by the inequality
$V_{\lambda}$
given by the inequality
This observation is enough to establish the well-known fact, that the local bound (i.e. (1) with
![]() $\delta=0$
) can not be improved for the sphere
$\delta=0$
) can not be improved for the sphere
![]() $X=S^2$
. So far we have only described the most basic version of the sup-norm problem which, is already very interesting on its own. In addition it admits many variations which have been studied throughout the years. An example for such a variation is the so called level aspect where the base manifold changes in some convenient family
$X=S^2$
. So far we have only described the most basic version of the sup-norm problem which, is already very interesting on its own. In addition it admits many variations which have been studied throughout the years. An example for such a variation is the so called level aspect where the base manifold changes in some convenient family
![]() $X_1,X_2,\ldots$
and one keeps track of this change in the sup-norm bound (1) using a suitable parameter called the level. Another generalisation that should be mentioned allows X to be a manifold of higher dimension and rank.
$X_1,X_2,\ldots$
and one keeps track of this change in the sup-norm bound (1) using a suitable parameter called the level. Another generalisation that should be mentioned allows X to be a manifold of higher dimension and rank.
Essentially any progress that has been made towards the sup-norm problem as introduced above relies on the arithmeticity of X. The basic idea introduced in the monumental paper [
Reference Iwaniec and Sarnak14
] is to employ additional symmetries (in the form of Hecke operators) to build a spectral projector that is sharper than the one constructed with only the Laplace–Beltrami operator at hand. Morally this might be thought of as forcing a multiplicity one situation even if the Laplace–Beltrami eigenspaces can not be rigorously controlled. The result of this method is a bound as in (1) with
![]() $\delta={1}/{12}$
for compact quotients
$\delta={1}/{12}$
for compact quotients
![]() $X=\Gamma\backslash \mathbb{H}$
constructed from maximal orders in quaternion algebras.
$X=\Gamma\backslash \mathbb{H}$
constructed from maximal orders in quaternion algebras.
Since its appearance the method from [
Reference Iwaniec and Sarnak14
] has been tweaked, modified and generalised, see for example [
Reference Assing1
,
Reference Blomer and Holowinsky6
,
Reference Blomer and Maga7
,
Reference Saha21
,
Reference Templier23
] and the references within. Much work is concerned with congruence quotients
![]() $X=\Gamma_0(N)\backslash \mathbb{H}$
on which so called Hecke–Maaß newforms are considered. Since these newforms enjoy a nice multiplicity one property they are natural candidates for the sup-norm problem. In this paper we are going beyond the case of newforms and consider situations where the dimension of the underlying eigenspace grows. In other words, we solve the sup-norm problem in the dimension aspect. This aspect is a new facet of the sup-norm problem which seems extremely interesting and is not yet well studied. While our result is the first in p-adic setting it is only preceded by [
Reference Blomer, Harcos, Maga and Milićević5
] where an archimedean version of this aspect is discussed.
$X=\Gamma_0(N)\backslash \mathbb{H}$
on which so called Hecke–Maaß newforms are considered. Since these newforms enjoy a nice multiplicity one property they are natural candidates for the sup-norm problem. In this paper we are going beyond the case of newforms and consider situations where the dimension of the underlying eigenspace grows. In other words, we solve the sup-norm problem in the dimension aspect. This aspect is a new facet of the sup-norm problem which seems extremely interesting and is not yet well studied. While our result is the first in p-adic setting it is only preceded by [
Reference Blomer, Harcos, Maga and Milićević5
] where an archimedean version of this aspect is discussed.
To explain our result and its connection to the work of Blomer, Harcos, Maga and Milićević it will be most convenient to leave the classical world of Hecke–Maaß-newforms behind and work in the language of automorphic forms and automorphic representations.
The sup-norm problem we will consider is connected to small
![]() $\operatorname{GL}_2(\mathbb{Z}_p)$
-types in cuspidal automorphic representations
$\operatorname{GL}_2(\mathbb{Z}_p)$
-types in cuspidal automorphic representations
![]() $\pi$
, where
$\pi$
, where
![]() $p>3$
is prime. Comparing this to the recent work [
Reference Blomer, Harcos, Maga and Milićević5
] we are replacing the archimedean place
$p>3$
is prime. Comparing this to the recent work [
Reference Blomer, Harcos, Maga and Milićević5
] we are replacing the archimedean place
![]() $\infty$
by a finite place p and the minimal U(2)-type of some automorphic representation by a suitably chosen
$\infty$
by a finite place p and the minimal U(2)-type of some automorphic representation by a suitably chosen
![]() $\operatorname{GL}_2(\mathbb{Z}_p)$
-type. Note that in order to afford interesting K-types at the archimedean place it is necessary to work over fields admitting complex places or in higher rank. In the p-adic world we already meet interesting cases when working with automorphic forms for
$\operatorname{GL}_2(\mathbb{Z}_p)$
-type. Note that in order to afford interesting K-types at the archimedean place it is necessary to work over fields admitting complex places or in higher rank. In the p-adic world we already meet interesting cases when working with automorphic forms for
![]() $\operatorname{GL}_2$
over
$\operatorname{GL}_2$
over
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
1·1. Set-up and main result
Before we continue our discussion we need to fix some notation. Let
![]() $G(R)=\operatorname{GL}_2(R)$
for some ring R and let
$G(R)=\operatorname{GL}_2(R)$
for some ring R and let
![]() $\mathbb{A}$
be the adele ring over
$\mathbb{A}$
be the adele ring over
![]() $\mathbb{Q}$
. We will be working with cuspidal automorphic representations
$\mathbb{Q}$
. We will be working with cuspidal automorphic representations
![]() $\pi$
of
$\pi$
of
![]() $G(\mathbb{A})$
with unitary central character
$G(\mathbb{A})$
with unitary central character
![]() $\omega_{\pi}$
. Abusing notation we will write
$\omega_{\pi}$
. Abusing notation we will write
![]() $\pi \subset L_0^2(G(\mathbb{Q})\backslash G(\mathbb{A}),\omega_{\pi})$
assuming that
$\pi \subset L_0^2(G(\mathbb{Q})\backslash G(\mathbb{A}),\omega_{\pi})$
assuming that
![]() $\pi$
acts on an irreducible subspace of cuspidal automorphic forms by right translation. Given a compact subgroup H we write
$\pi$
acts on an irreducible subspace of cuspidal automorphic forms by right translation. Given a compact subgroup H we write
![]() $\pi^H$
for the space of H-invariant elements in
$\pi^H$
for the space of H-invariant elements in
![]() $\pi$
.
$\pi$
.
Set
![]() $K_{\infty}=SO(2)$
and
$K_{\infty}=SO(2)$
and
![]() $K_l=\operatorname{GL}_2(\mathbb{Z}_l)$
for primes l. Combining these we get the compact subgroup
$K_l=\operatorname{GL}_2(\mathbb{Z}_l)$
for primes l. Combining these we get the compact subgroup
![]() $K=\prod_v K_v\subset G(\mathbb{A})$
. Given a prime
$K=\prod_v K_v\subset G(\mathbb{A})$
. Given a prime
![]() $p>3$
and
$p>3$
and
![]() $m>0$
we consider the smaller compact subgroup
$m>0$
we consider the smaller compact subgroup
Note that
![]() $K(p^m)$
is normal and of finite index in K.
$K(p^m)$
is normal and of finite index in K.
Throughout we restrict ourselves to the situation where
![]() $\pi$
is unramified (i.e. spherical) away from p. In particular it is spherical at
$\pi$
is unramified (i.e. spherical) away from p. In particular it is spherical at
![]() $\infty$
and one associates the spectral parameter
$\infty$
and one associates the spectral parameter
![]() $t_{\pi}$
. Set
$t_{\pi}$
. Set
![]() $T=1+\lvert{t_{\pi}}\rvert$
. Further, we have
$T=1+\lvert{t_{\pi}}\rvert$
. Further, we have
We set
![]() $V=\pi^{K(p^{m_{\pi}})}$
and observe that
$V=\pi^{K(p^{m_{\pi}})}$
and observe that
![]() $\pi\vert_K$
endows V with the structure of a K-module. It turns out that, if
$\pi\vert_K$
endows V with the structure of a K-module. It turns out that, if
![]() $\pi$
is twist minimal, V is irreducible (see Lemma 2·2 below). Set
$\pi$
is twist minimal, V is irreducible (see Lemma 2·2 below). Set
![]() $d=\dim_{\mathbb{C}}V$
, choose an orthonormal basis
$d=\dim_{\mathbb{C}}V$
, choose an orthonormal basis
![]() $\phi_1,\ldots,\phi_d$
for V with respect to the
$\phi_1,\ldots,\phi_d$
for V with respect to the
![]() $L^2_0(G(\mathbb{Q})\backslash G(\mathbb{A}),\omega_{\pi})$
inner product. Define
$L^2_0(G(\mathbb{Q})\backslash G(\mathbb{A}),\omega_{\pi})$
inner product. Define
 \begin{equation*} \Phi(g) = \left( \sum_{i=1}^d \lvert{\phi_i(g)}\rvert^2\right)^{\frac{1}{2}},\end{equation*}
\begin{equation*} \Phi(g) = \left( \sum_{i=1}^d \lvert{\phi_i(g)}\rvert^2\right)^{\frac{1}{2}},\end{equation*}
which is independent of the choice of the orthonormal basis
![]() $\phi_1,\ldots,\phi_d$
. We are concerned with the sup-norm of
$\phi_1,\ldots,\phi_d$
. We are concerned with the sup-norm of
![]() $\Phi(g)$
and obtain the following theorem which is a close analogue to [
Reference Blomer, Harcos, Maga and Milićević5
, theorem 1].
$\Phi(g)$
and obtain the following theorem which is a close analogue to [
Reference Blomer, Harcos, Maga and Milićević5
, theorem 1].
Theorem 1·1. Let
![]() $p>3$
be prime and suppose
$p>3$
be prime and suppose
![]() $\pi$
is twist minimal. In the notation above we have
$\pi$
is twist minimal. In the notation above we have
If the (arithmetic)-conductor of
![]() $\pi$
is a perfect square (i.e. the exponent-conductor of the p-component
$\pi$
is a perfect square (i.e. the exponent-conductor of the p-component
![]() $\pi_p$
of
$\pi_p$
of
![]() $\pi$
is even) or the p-component
$\pi$
is even) or the p-component
![]() $\pi_p$
of
$\pi_p$
of
![]() $\pi$
is not supercuspidal, then we have the better bound
$\pi$
is not supercuspidal, then we have the better bound
While in the spectral aspect (i.e. the T-aspect in our statement) we only recover the local bound, the key feature of our theorem is the sub-local exponent in the dimension aspect d. Given the obstruction to the sup-norm problem coming from growing eigenspaces the aspect under consideration may seem counter intuitive. However, we are letting the dimension of the eigenspace vary in a controlled manner and manage to show that one can still achieve a considerable power saving in d on average over any orthonormal basis.
Note that the sup-norm bound given in the theorem holds globally. Thus, unlike the one in [
Reference Blomer, Harcos, Maga and Milićević5
, theorem 1], no restriction to a compact domain is necessary here. As usual when proving global sup-norm bound the argument consists of two steps. First, a bound via the Whittaker expansion takes care of the regions close to the cusps. This part of the argument is fairly standard but requires some new computations of ramified Whittaker vectors. Second, a bound obtained from the amplified pre-trace inequality is used to handle the bulk. At this point it becomes crucial that we are only treating the average function
![]() $\Phi$
. Indeed, this allows us to identify the test function on the geometric side as a character of a finite group. The analysis of this character is carried out in Lemma 4·4 below and relies on character tables given in [
Reference Kutzko15
]. This is the only place where the assumption
$\Phi$
. Indeed, this allows us to identify the test function on the geometric side as a character of a finite group. The analysis of this character is carried out in Lemma 4·4 below and relies on character tables given in [
Reference Kutzko15
]. This is the only place where the assumption
![]() $p>3$
is used.
$p>3$
is used.
To end this section let us briefly discuss the numerology of the exponents in the d-aspect. For simplicity we restrict this discussion to the cases in which our result gives the strong bound (3). Let us start by talking about the local- (not to say trivial-) bound (in the bulk). To obtain this we can follow Marshall’s strategy (see [
Reference Marshall18
]) which leads to the following. Let F be any cuspidal automorphic form so that the translates
![]() $\phi(\!\cdot k)$
,
$\phi(\!\cdot k)$
,
![]() $k\in K$
, generate an irreducible K-module
$k\in K$
, generate an irreducible K-module
![]() $W_F$
. Then choosing certain K-matrix-coefficients as test functions in the pre-trace inequality yields
$W_F$
. Then choosing certain K-matrix-coefficients as test functions in the pre-trace inequality yields
Applying this to
![]() $\Phi$
upon noting that
$\Phi$
upon noting that
![]() $\Vert \Phi \Vert_2= d^{\frac{1}{2}}$
suggests the local bound
$\Vert \Phi \Vert_2= d^{\frac{1}{2}}$
suggests the local bound
(The same bound can also be obtained from the Whittaker expansion coupled with a suitable generating domain.) Thus amplification allows us to improve the exponent from the local bound by
![]() ${1}/{6}$
, which should be an familiar exponent. More suggestively we can write our main result as
${1}/{6}$
, which should be an familiar exponent. More suggestively we can write our main result as
One could say that Theorem 1·1 implies
![]() $\Vert \phi_i\Vert_{\infty}\ll d^{\frac{1}{3}}$
on average. Note that if
$\Vert \phi_i\Vert_{\infty}\ll d^{\frac{1}{3}}$
on average. Note that if
![]() $p^{m_{\pi}}$
agrees with the arithmetic conductor
$p^{m_{\pi}}$
agrees with the arithmetic conductor
![]() $p^{n_{\pi}}$
of
$p^{n_{\pi}}$
of
![]() $\pi$
, then this result is not very interesting. Indeed, in this case we can generate the elements
$\pi$
, then this result is not very interesting. Indeed, in this case we can generate the elements
![]() $\phi_1,\ldots,\phi_d$
in V directly from the newform
$\phi_1,\ldots,\phi_d$
in V directly from the newform
![]() $\phi_{\circ}$
in
$\phi_{\circ}$
in
![]() $\pi$
. By now there are very good bounds for this newform (and thus also for the
$\pi$
. By now there are very good bounds for this newform (and thus also for the
![]() $\phi_i$
’s) known in the literature. See [
Reference Templier23
] if
$\phi_i$
’s) known in the literature. See [
Reference Templier23
] if
![]() $m_{\pi}=n_{\pi}=1$
or [
Reference Comtat9
] in general. However, in the remaining cases (since
$m_{\pi}=n_{\pi}=1$
or [
Reference Comtat9
] in general. However, in the remaining cases (since
![]() $\pi$
is assumed to be twist minimal these correspond to the situation where
$\pi$
is assumed to be twist minimal these correspond to the situation where
![]() $\pi$
is supercuspidal at p) our result provides new information in the sup-norm problem. Indeed one can still generate V from a translate of the newfom
$\pi$
is supercuspidal at p) our result provides new information in the sup-norm problem. Indeed one can still generate V from a translate of the newfom
![]() $\phi_{\circ}$
. (This is precisely the strategy used in [
Reference Marshall18
,
Reference Saha21
] to derive local bounds for the newform of arbitrary level using (4).) Translated into the level-aspect our result now essentially says that the sup-norm of the
$\phi_{\circ}$
. (This is precisely the strategy used in [
Reference Marshall18
,
Reference Saha21
] to derive local bounds for the newform of arbitrary level using (4).) Translated into the level-aspect our result now essentially says that the sup-norm of the
![]() $\phi_i$
’s is bounded by
$\phi_i$
’s is bounded by
![]() $p^{\frac{1}{3}\lceil \frac{n_{\pi}}{2}\rceil}$
on average. To the best of our knowledge this can not be derived from any known sup-norm results on the newform
$p^{\frac{1}{3}\lceil \frac{n_{\pi}}{2}\rceil}$
on average. To the best of our knowledge this can not be derived from any known sup-norm results on the newform
![]() $\phi_{\circ}$
.
$\phi_{\circ}$
.
Finally we want to compare our result to the guiding archimedean example [
Reference Blomer, Harcos, Maga and Milićević5
, theorem 1]. Recall that we need to replace the K-module V by some irreducible U(2) representation W. This representation W will occur as the minimal U(2)-type in some cuspidal automorphic
![]() $\pi$
of
$\pi$
of
![]() $G(\mathbb{A}_{\mathbb{Q}(i)})$
. Note that if
$G(\mathbb{A}_{\mathbb{Q}(i)})$
. Note that if
![]() $\dim_{\mathbb{C}}W\asymp l$
we can think of
$\dim_{\mathbb{C}}W\asymp l$
we can think of
![]() $\pi$
(or rather
$\pi$
(or rather
![]() $\pi_{\infty}$
) having spectral density
$\pi_{\infty}$
) having spectral density
![]() $\asymp l^2$
. This explains the local bounds
$\asymp l^2$
. This explains the local bounds
where
![]() $\Phi$
is constructed as an average over some suitable basis of W similar to our construction above. As result of an amplification process the authors of [
Reference Blomer, Harcos, Maga and Milićević5
] arrive at
$\Phi$
is constructed as an average over some suitable basis of W similar to our construction above. As result of an amplification process the authors of [
Reference Blomer, Harcos, Maga and Milićević5
] arrive at
Our notation suggests that in the result from [
Reference Blomer, Harcos, Maga and Milićević5
] the number
![]() $l^2$
playes the role of our d. This can be explained via the spectral density of
$l^2$
playes the role of our d. This can be explained via the spectral density of
![]() $\pi_{\infty}$
and respectively
$\pi_{\infty}$
and respectively
![]() $\pi_p$
. Indeed while in the archimedean situation the spectral density is roughly
$\pi_p$
. Indeed while in the archimedean situation the spectral density is roughly
![]() $l^2$
in our case the spectral density is linearly related to d. Thus in both cases the square root of the spectral density seems to determine the trivial bound. (This is only reasonable because we are considering minimal or close to minimal K-types in both cases.) Note that the quality of the saving
$l^2$
in our case the spectral density is linearly related to d. Thus in both cases the square root of the spectral density seems to determine the trivial bound. (This is only reasonable because we are considering minimal or close to minimal K-types in both cases.) Note that the quality of the saving
![]() $1/6$
in the p-adic versus
$1/6$
in the p-adic versus
![]() $1/12$
in the archimedean case comes from slightly different behaviour of the spectral transform.
$1/12$
in the archimedean case comes from slightly different behaviour of the spectral transform.
Finally, let us remark that if the exponent conductor of
![]() $\pi_p$
is odd and
$\pi_p$
is odd and
![]() $\pi_p$
is supercuspidal, then our bounds for the spectral transform, which in this case are linked to certain badly-behaved characters of
$\pi_p$
is supercuspidal, then our bounds for the spectral transform, which in this case are linked to certain badly-behaved characters of
![]() $\operatorname{GL}_2$
over finite rings, are comparable to those used in [
Reference Blomer, Harcos, Maga and Milićević5
]. This explains that in this case we have matching numerology and obtain only a saving of
$\operatorname{GL}_2$
over finite rings, are comparable to those used in [
Reference Blomer, Harcos, Maga and Milićević5
]. This explains that in this case we have matching numerology and obtain only a saving of
![]() ${1}/{12}$
in the final exponent. Translated to the level aspect our result states that on average the
${1}/{12}$
in the final exponent. Translated to the level aspect our result states that on average the
![]() $\phi_i$
’s are bounded by
$\phi_i$
’s are bounded by
![]() $p^{\frac{5(n_{\pi}+1)}{24}}$
. Bounds of this quality are known for newforms only in the compact setting, see [
Reference Hu and Saha13
].
$p^{\frac{5(n_{\pi}+1)}{24}}$
. Bounds of this quality are known for newforms only in the compact setting, see [
Reference Hu and Saha13
].
Remark 1·2. Questions of these type should be even more interesting when considered in higher rank. The reason is that in higher rank the analogously defined small K-types can not be generated from translates of the newform. For example if one considers a depth-zero supercuspidal representation
![]() $\pi_p$
of
$\pi_p$
of
![]() $\operatorname{GL}_3(\mathbb{Q}_p)$
, then it has (arithmetic)-conductor
$\operatorname{GL}_3(\mathbb{Q}_p)$
, then it has (arithmetic)-conductor
![]() $p^3$
and the space
$p^3$
and the space
![]() $\pi_p^{K_p^{(3)}(1)}$
, where
$\pi_p^{K_p^{(3)}(1)}$
, where
![]() $K_p^{(3)}(1)$
is the principal congruence subgroup modulo p in
$K_p^{(3)}(1)$
is the principal congruence subgroup modulo p in
![]() $\operatorname{GL}_3(\mathbb{Z}_p)$
, is non-zero. However, it seems impossible to find a translate of the newform that generates
$\operatorname{GL}_3(\mathbb{Z}_p)$
, is non-zero. However, it seems impossible to find a translate of the newform that generates
![]() $\pi_p^{K_p^{(3)}(1)}$
. Indeed this would mean finding
$\pi_p^{K_p^{(3)}(1)}$
. Indeed this would mean finding
![]() $g\in \operatorname{GL}_3(\mathbb{Q}_p)$
with
$g\in \operatorname{GL}_3(\mathbb{Q}_p)$
with
 \begin{align*}K_p^{(3)}(1)\subset g^{-1}\left[ \begin{matrix} \mathbb{Z}_p & \mathbb{Z}_p & \mathbb{Z}_p \\ \mathbb{Z}_p & \mathbb{Z}_p & \mathbb{Z}_p \\ p\mathbb{Z}_p & p\mathbb{Z}_p & 1+p\mathbb{Z}_p\end{matrix}\right] g.\end{align*}
\begin{align*}K_p^{(3)}(1)\subset g^{-1}\left[ \begin{matrix} \mathbb{Z}_p & \mathbb{Z}_p & \mathbb{Z}_p \\ \mathbb{Z}_p & \mathbb{Z}_p & \mathbb{Z}_p \\ p\mathbb{Z}_p & p\mathbb{Z}_p & 1+p\mathbb{Z}_p\end{matrix}\right] g.\end{align*}
However, the question treated in this paper still makes sense and trying to answer it is work in progress.
2. Preliminary considerations
In this section we are putting in some ground work on which the following sections will rely.
Recall that
![]() $\pi$
was a cuspidal automorphic representation. Since we are assuming that
$\pi$
was a cuspidal automorphic representation. Since we are assuming that
![]() $\pi_v$
is unramified for
$\pi_v$
is unramified for
![]() $v\neq p$
, the (arithmetic)-conductor of
$v\neq p$
, the (arithmetic)-conductor of
![]() $\pi$
is
$\pi$
is
![]() $p^{n_{\pi}}$
for
$p^{n_{\pi}}$
for
![]() $n_{\pi}\in \mathbb{N}\cup\{0\}$
. When
$n_{\pi}\in \mathbb{N}\cup\{0\}$
. When
![]() $n_{\pi}=0$
we have
$n_{\pi}=0$
we have
![]() $d=1$
and our theorem reduces to the local bound in the spectral aspect, so that without loss of generality we can assume
$d=1$
and our theorem reduces to the local bound in the spectral aspect, so that without loss of generality we can assume
![]() $n_{\pi}\geq 1$
throughout. By Flath’s factorisation theorem we can fix an isomorphism
$n_{\pi}\geq 1$
throughout. By Flath’s factorisation theorem we can fix an isomorphism
![]() $\pi \cong \bigotimes \pi_v$
. Note that also the central character of
$\pi \cong \bigotimes \pi_v$
. Note that also the central character of
![]() $\pi$
factors as
$\pi$
factors as
![]() $\omega_{\pi}=\bigotimes_v \omega_{\pi_v}$
where
$\omega_{\pi}=\bigotimes_v \omega_{\pi_v}$
where
![]() $\omega_{\pi_v}$
is the central character of
$\omega_{\pi_v}$
is the central character of
![]() $\pi_v$
. For
$\pi_v$
. For
![]() $v\neq p$
we can fix a spherical (i.e.
$v\neq p$
we can fix a spherical (i.e.
![]() $K_v$
-invariant vector)
$K_v$
-invariant vector)
![]() $\phi_v^{\circ}\in \pi_v^{K_v}$
. This vector is unique up to scaling. Recall that
$\phi_v^{\circ}\in \pi_v^{K_v}$
. This vector is unique up to scaling. Recall that
![]() $\phi_i$
,
$\phi_i$
,
![]() $i=1,\ldots,d$
forms an orthonormal basis of
$i=1,\ldots,d$
forms an orthonormal basis of
![]() $V=\pi^{K(p^{m_{\pi}})}$
. Thus there is
$V=\pi^{K(p^{m_{\pi}})}$
. Thus there is
![]() $\phi_p^{(i)}$
so that we can identify
$\phi_p^{(i)}$
so that we can identify
Since the spherical functions
![]() $\phi_p^{\circ}$
are well understood much of our work boils down to understanding properties of an orthogonal basis
$\phi_p^{\circ}$
are well understood much of our work boils down to understanding properties of an orthogonal basis
This a purely local problem, which we investigate in the following subsection.
2·1. Local considerations
We now focus on properties of the local representation
![]() $\pi_p$
. We start by recalling the classification of local representations. But before we do so we need some more notation. Given a (quasi)-character
$\pi_p$
. We start by recalling the classification of local representations. But before we do so we need some more notation. Given a (quasi)-character
![]() $\chi\colon \mathbb{Q}_p^{\times}\to \mathbb{C}^{\times}$
we write
$\chi\colon \mathbb{Q}_p^{\times}\to \mathbb{C}^{\times}$
we write
![]() $a(\chi)$
for the (exponent)-conductor. Further write
$a(\chi)$
for the (exponent)-conductor. Further write
for an Iwahori subgroup. Let
![]() $K_p'=N_{G(\mathbb{Q}_p)}(I_0(p))$
be the normaliser of
$K_p'=N_{G(\mathbb{Q}_p)}(I_0(p))$
be the normaliser of
![]() $I_0(p)$
in
$I_0(p)$
in
![]() $G(\mathbb{Q}_p)$
. We also need the filtration
$G(\mathbb{Q}_p)$
. We also need the filtration
of
![]() $K_p'$
by normal subgroups. Finally given two quasi characters
$K_p'$
by normal subgroups. Finally given two quasi characters
![]() $\chi_1,\chi_2\colon \mathbb{Q}_p^{\times}\to\mathbb{C}^{\times}$
we form the (normalised) induced representation on
$\chi_1,\chi_2\colon \mathbb{Q}_p^{\times}\to\mathbb{C}^{\times}$
we form the (normalised) induced representation on
![]() $\operatorname{Ind}_B^{G(\mathbb{Q}_p)}(\chi_1\otimes \chi_2)$
as usual. If this representation is irreducible, then we denote the so obtained representation by
$\operatorname{Ind}_B^{G(\mathbb{Q}_p)}(\chi_1\otimes \chi_2)$
as usual. If this representation is irreducible, then we denote the so obtained representation by
![]() $\chi_1\boxplus\chi_2$
. We write St for the Steinberg representation which we may identify with the unique irreducible subspace of
$\chi_1\boxplus\chi_2$
. We write St for the Steinberg representation which we may identify with the unique irreducible subspace of
![]() $\operatorname{Ind}_B^{G(\mathbb{Q}_p)}(\lvert{\cdot}\rvert^{\frac{1}{2}}\otimes \lvert{\cdot}\rvert^{-\frac{1}{2}})$
. We are now ready to recite the following well-known classification.
$\operatorname{Ind}_B^{G(\mathbb{Q}_p)}(\lvert{\cdot}\rvert^{\frac{1}{2}}\otimes \lvert{\cdot}\rvert^{-\frac{1}{2}})$
. We are now ready to recite the following well-known classification.
Lemma 2·1. The representation
![]() $\pi_p$
falls into one of the following three cases:
$\pi_p$
falls into one of the following three cases:
-
(i) Case 1 (Principal series): there are (quasi)-characters
 $\chi_i\colon \mathbb{Q}_p^{\times}\to \mathbb{C}^{\times}$
such that
$\chi_i\colon \mathbb{Q}_p^{\times}\to \mathbb{C}^{\times}$
such that
 $\chi_1\chi_2=\omega_{\pi_p}$
,
$\chi_1\chi_2=\omega_{\pi_p}$
,
 $a(\chi_1)+a(\chi_2)=n_{\pi}$
and
$a(\chi_1)+a(\chi_2)=n_{\pi}$
and
 $\pi_p = \chi_1\boxplus \chi_2$
.
$\pi_p = \chi_1\boxplus \chi_2$
. -
(ii) Case 2 (special): there is a (quasi)-character
 $\chi\colon \mathbb{Q}_p^{\times}\to \mathbb{C}^{\times}$
with
$\chi\colon \mathbb{Q}_p^{\times}\to \mathbb{C}^{\times}$
with
 $n_{\pi}=2a(\chi)$
if
$n_{\pi}=2a(\chi)$
if
 $a(\chi)>0$
or
$a(\chi)>0$
or
 $n_{\pi}=1$
otherwise,
$n_{\pi}=1$
otherwise,
 $\chi^2=\omega_{\pi_p}$
and
$\chi^2=\omega_{\pi_p}$
and
 $\pi_p=\chi\otimes \text{St}$
.
$\pi_p=\chi\otimes \text{St}$
. -
(iii) Case 3 (Supercuspidal): the representation
 $\pi_p$
is supercuspidal. In this case we can write
$\pi_p$
is supercuspidal. In this case we can write
 $\pi_p=\chi \cdot \pi_p'$
for a (quasi)-character
$\pi_p=\chi \cdot \pi_p'$
for a (quasi)-character
 $\chi\colon \mathbb{Q}_p^{\times}\to\mathbb{C}^{\times}$
and some twist-minimal representation
$\chi\colon \mathbb{Q}_p^{\times}\to\mathbb{C}^{\times}$
and some twist-minimal representation
 $\pi_p'$
of conductor
$\pi_p'$
of conductor
 $n_{\pi}'$
which is constructed in one of the following two ways:
$n_{\pi}'$
which is constructed in one of the following two ways:-
(a) Case 3.1 (
 $n_{\pi}'$
even): there is an irreducible representation
$n_{\pi}'$
even): there is an irreducible representation
 $\tau$
of
$\tau$
of
 $Z\cdot K_p$
with
$Z\cdot K_p$
with
 $\tau\vert_{Z} = \chi^{-2}\cdot \omega_{\pi_p}$
which factors through
$\tau\vert_{Z} = \chi^{-2}\cdot \omega_{\pi_p}$
which factors through
 $K_p({n_{\pi}'}/{2})$
so that
$K_p({n_{\pi}'}/{2})$
so that
 $\pi_p' = c-\operatorname{Ind}_{ZK_p}^{G(\mathbb{Q}_p)}\tau$
.
$\pi_p' = c-\operatorname{Ind}_{ZK_p}^{G(\mathbb{Q}_p)}\tau$
. -
(b) Case 3.2 (
 $n_{\pi}'$
odd): there is an irreducible representation
$n_{\pi}'$
odd): there is an irreducible representation
 $\tau$
of
$\tau$
of
 $K_p'$
which is invariant by
$K_p'$
which is invariant by
 $K_p'(n_{\pi}'-1)$
with
$K_p'(n_{\pi}'-1)$
with
 $\tau\vert_Z=\chi^{-2}\cdot \omega_{\pi_p}$
such that
$\tau\vert_Z=\chi^{-2}\cdot \omega_{\pi_p}$
such that
 $\pi_p'=c-\operatorname{Ind}_{K_p'}^{G(\mathbb{Q}_p)}\tau$
.
$\pi_p'=c-\operatorname{Ind}_{K_p'}^{G(\mathbb{Q}_p)}\tau$
.
-
With this classification at hand we continue to study the subspaces V in more detail.
Lemma 2·2. Suppose
![]() $\pi_p$
is twist minimal and let
$\pi_p$
is twist minimal and let
![]() $m_{\pi}$
be as in (2), then
$m_{\pi}$
be as in (2), then
![]() $V=\pi_p^{K(m_{\pi})}$
is irreducible as
$V=\pi_p^{K(m_{\pi})}$
is irreducible as
![]() $K_p$
-module and we have:
$K_p$
-module and we have:
-
(i) the invariant
 $m_{\pi}$
is given by
$m_{\pi}$
is given by  \begin{align*}m_{\pi}=\begin{cases} n_{\pi} &\text{ if } \pi_p \text{ is Case 1},\\ \lfloor \frac{n_{\pi}+1}{2}\rfloor & \text{ if }\pi_p \text{ is Case 2,3;}\end{cases}\end{align*}
\begin{align*}m_{\pi}=\begin{cases} n_{\pi} &\text{ if } \pi_p \text{ is Case 1},\\ \lfloor \frac{n_{\pi}+1}{2}\rfloor & \text{ if }\pi_p \text{ is Case 2,3;}\end{cases}\end{align*}
-
(ii) the dimension of V is given by
 \begin{align*}d= p^{m_{\pi}}\cdot \begin{cases} (1+\frac{1}{p}) &\text{ if $\pi_p$ is Case 1,}\\1 &\text{ if $\pi_p$ is Case 2,} \\ (1-\frac{1}{p}) &\text{ if $\pi_p$ is Case 3$\cdot$1 and }\\ (1-\frac{1}{p^2}) &\text{ if $\pi_p$ is Case 3$\cdot$2;} \end{cases}\end{align*}
\begin{align*}d= p^{m_{\pi}}\cdot \begin{cases} (1+\frac{1}{p}) &\text{ if $\pi_p$ is Case 1,}\\1 &\text{ if $\pi_p$ is Case 2,} \\ (1-\frac{1}{p}) &\text{ if $\pi_p$ is Case 3$\cdot$1 and }\\ (1-\frac{1}{p^2}) &\text{ if $\pi_p$ is Case 3$\cdot$2;} \end{cases}\end{align*}
Proof. This is not new and we only have to ensemble the pieces appropriately. Let us proceed case by case.
First, if
![]() $\pi_p$
is in Case 1, then twist-minimality implies that
$\pi_p$
is in Case 1, then twist-minimality implies that
![]() $\chi_2$
(or similarly
$\chi_2$
(or similarly
![]() $\chi_1$
) is unramified. Thus we have
$\chi_1$
) is unramified. Thus we have
![]() $n_{\pi}=a(\chi_1)$
and the results on d and
$n_{\pi}=a(\chi_1)$
and the results on d and
![]() $m_{\pi}$
follow from [
Reference Miyauchi and Yamauchi20
, proposition 4.3]. Irreducibility can be seen by direct computation.
$m_{\pi}$
follow from [
Reference Miyauchi and Yamauchi20
, proposition 4.3]. Irreducibility can be seen by direct computation.
Second, if
![]() $\pi_p$
is in Case 2 and twist minimal, then
$\pi_p$
is in Case 2 and twist minimal, then
![]() $\pi_p = \text{St}$
and
$\pi_p = \text{St}$
and
![]() $n_{\pi}=1$
. The results on d and
$n_{\pi}=1$
. The results on d and
![]() $m_{\pi}$
follow again from [
Reference Miyauchi and Yamauchi20
, proposition 4.3]. In this case irreducibility follows from [
Reference Casselman8
, theorem 1].
$m_{\pi}$
follow again from [
Reference Miyauchi and Yamauchi20
, proposition 4.3]. In this case irreducibility follows from [
Reference Casselman8
, theorem 1].
Finally, if
![]() $\pi_p$
belongs to Case 3, then the full statement is given in [
Reference Loeffler and Weinstein17
, theorem 3·5]. (See also [
Reference Miyauchi and Yamauchi20
, lemma 4·5, corollary 4·7] for the computation of
$\pi_p$
belongs to Case 3, then the full statement is given in [
Reference Loeffler and Weinstein17
, theorem 3·5]. (See also [
Reference Miyauchi and Yamauchi20
, lemma 4·5, corollary 4·7] for the computation of
![]() $m_{\pi}$
and d.)
$m_{\pi}$
and d.)
2·2. A generating domain
We now switch to the global picture again and aim to produce a suitable set
![]() $\mathcal{F}\subset G(\mathbb{A})$
which reduces our problem to studying
$\mathcal{F}\subset G(\mathbb{A})$
which reduces our problem to studying
Let
![]() $\mathcal{F}$
be the standard fundamental domain for
$\mathcal{F}$
be the standard fundamental domain for
![]() $\operatorname{SL}_2(\mathbb{Z})\backslash \mathbb{H}$
, which we identify with a subset of
$\operatorname{SL}_2(\mathbb{Z})\backslash \mathbb{H}$
, which we identify with a subset of
![]() $\operatorname{GL}_2(\mathbb{R})$
by identifying
$\operatorname{GL}_2(\mathbb{R})$
by identifying
![]() $z=x+iy\in\mathbb{H}$
with
$z=x+iy\in\mathbb{H}$
with
![]() $n(x)a(y)\in B(\mathbb{R})\subset\operatorname{GL}_2(\mathbb{R})$
. Here
$n(x)a(y)\in B(\mathbb{R})\subset\operatorname{GL}_2(\mathbb{R})$
. Here
We further view
![]() $\mathcal{F}$
as a subset of
$\mathcal{F}$
as a subset of
![]() $G(\mathbb{A})$
by identifying it with its image under the usual embedding
$G(\mathbb{A})$
by identifying it with its image under the usual embedding
![]() $G(\mathbb{R}) \to G(\mathbb{A})$
. The same series of identifications allows us to write
$G(\mathbb{R}) \to G(\mathbb{A})$
. The same series of identifications allows us to write
![]() $\Phi(z)$
for
$\Phi(z)$
for
![]() $z\in \mathbb{H}$
.
$z\in \mathbb{H}$
.
Lemma 2·3. We have
Proof. First we take
![]() $g\in G(\mathbb{A})$
and observe that by strong approximation we can write
$g\in G(\mathbb{A})$
and observe that by strong approximation we can write
We directly obtain
![]() $\lvert{\phi_i(g)}\rvert=\lvert{\phi_i(bk)}\rvert$
by automorphy and the action of Z via a unitary character. However, we now observe that if
$\lvert{\phi_i(g)}\rvert=\lvert{\phi_i(bk)}\rvert$
by automorphy and the action of Z via a unitary character. However, we now observe that if
![]() $\phi_1,\ldots,\phi_d$
forms an orthonormal basis of V, then so does
$\phi_1,\ldots,\phi_d$
forms an orthonormal basis of V, then so does
![]() $\pi(k)\phi_1,\ldots, \pi(k)\phi_d$
. Let us write
$\pi(k)\phi_1,\ldots, \pi(k)\phi_d$
. Let us write
![]() $\Phi^{(k)}$
for the average constructed from the latter basis. Recall that
$\Phi^{(k)}$
for the average constructed from the latter basis. Recall that
![]() $\Phi$
was independent of the choice of the underlying orthonormal basis, so that we have
$\Phi$
was independent of the choice of the underlying orthonormal basis, so that we have
![]() $\Phi^{(k)}=\Phi$
. We conclude that
$\Phi^{(k)}=\Phi$
. We conclude that
3. The Whittaker bound
We will now start the process of deriving a first bound for
![]() $\Phi$
which will be valid (high) up in the cusp. This is done by estimating
$\Phi$
which will be valid (high) up in the cusp. This is done by estimating
![]() $\Phi$
using the Whittaker expansions of the
$\Phi$
using the Whittaker expansions of the
![]() $\phi_i$
’s. Throughout we will be working with an arbitrary orthogonal basis
$\phi_i$
’s. Throughout we will be working with an arbitrary orthogonal basis
![]() $\phi_1,\ldots,\phi_d$
and consider only
$\phi_1,\ldots,\phi_d$
and consider only
![]() $g\in \mathcal{F}$
.
$g\in \mathcal{F}$
.
3·1. Reduction to a local problem
Let
![]() $\phi=\phi_i$
for some
$\phi=\phi_i$
for some
![]() $i=1,\ldots, d$
. The global Whittaker period is given by
$i=1,\ldots, d$
. The global Whittaker period is given by
where
![]() $\psi_{\mathbb{A}}$
is the standard character of
$\psi_{\mathbb{A}}$
is the standard character of
![]() $\mathbb{Q}\backslash\mathbb{A}$
which has a factorisation
$\mathbb{Q}\backslash\mathbb{A}$
which has a factorisation
![]() $\psi_{\mathbb{A}} = \bigotimes_{v}\psi_v$
for
$\psi_{\mathbb{A}} = \bigotimes_{v}\psi_v$
for
![]() $\psi_{\infty}(x_{\infty}) = e(x_{\infty})$
and
$\psi_{\infty}(x_{\infty}) = e(x_{\infty})$
and
![]() $\psi_l$
unramified for all primes l. Note that
$\psi_l$
unramified for all primes l. Note that
![]() $W_{\phi}(\!\cdot)$
is right
$W_{\phi}(\!\cdot)$
is right
![]() $K(p^{m_{\pi}})$
-invariant and transforms with respect to
$K(p^{m_{\pi}})$
-invariant and transforms with respect to
![]() $\psi_{\mathbb{A}}$
when acted on by
$\psi_{\mathbb{A}}$
when acted on by
![]() $N(\mathbb{A})$
from the left. Thus a standard trick shows that
$N(\mathbb{A})$
from the left. Thus a standard trick shows that
![]() $W_{\phi}(a(q)g_{\infty})=0$
unless
$W_{\phi}(a(q)g_{\infty})=0$
unless
![]() $0\neq q\in \frac{1}{p^{m_{\pi}}}\mathbb{Z}$
. Indeed, for any x with
$0\neq q\in \frac{1}{p^{m_{\pi}}}\mathbb{Z}$
. Indeed, for any x with
![]() $n(x)\in K(p^{m_{\pi}})$
, one computes
$n(x)\in K(p^{m_{\pi}})$
, one computes
we conclude that, if
![]() $W(a(q)g_{\infty})\neq 0$
, then we have
$W(a(q)g_{\infty})\neq 0$
, then we have
![]() $\psi_{\mathbb{A}}(xq)=1$
for all such x. This gives precisely the condition
$\psi_{\mathbb{A}}(xq)=1$
for all such x. This gives precisely the condition
![]() $q\in {1}/{p^{m_{\pi}}}\mathbb{Z}$
.
$q\in {1}/{p^{m_{\pi}}}\mathbb{Z}$
.
This observation leads to the Whittaker expansion
 \begin{equation} \phi(g_{\infty}) = \sum_{n\in \mathbb{Z}\setminus \{0\}} W_{\phi}\left(a(\frac{n}{p^{m_{\pi}}})g_{\infty}\right).\nonumber\end{equation}
\begin{equation} \phi(g_{\infty}) = \sum_{n\in \mathbb{Z}\setminus \{0\}} W_{\phi}\left(a(\frac{n}{p^{m_{\pi}}})g_{\infty}\right).\nonumber\end{equation}
We need to exploit the factorisation of the Whittaker function
![]() $W_{\phi}$
. To do so we first observe that we have the factorisation of Whittaker models
$W_{\phi}$
. To do so we first observe that we have the factorisation of Whittaker models
Using the factorisation of
![]() $\phi$
will now determine distinguished elements in the local Whittaker models as follows. Starting at
$\phi$
will now determine distinguished elements in the local Whittaker models as follows. Starting at
![]() $v=\infty$
we set
$v=\infty$
we set
 \begin{equation} W_v(n(x)a(y)) = \frac{\lvert{y}\rvert^{\frac{1}{2}}K_{it_{\pi}}(2\pi\lvert{y}\rvert)}{2\lvert{\Gamma(\frac{1}{2}+it_{\pi})\Gamma(\frac{1}{2}-it_{\pi})}\rvert^{\frac{1}{2}}}e(x),\nonumber\end{equation}
\begin{equation} W_v(n(x)a(y)) = \frac{\lvert{y}\rvert^{\frac{1}{2}}K_{it_{\pi}}(2\pi\lvert{y}\rvert)}{2\lvert{\Gamma(\frac{1}{2}+it_{\pi})\Gamma(\frac{1}{2}-it_{\pi})}\rvert^{\frac{1}{2}}}e(x),\nonumber\end{equation}
where
![]() $t_{\pi}$
is the spectral parameter of
$t_{\pi}$
is the spectral parameter of
![]() $\pi_{\infty}$
. Of course
$\pi_{\infty}$
. Of course
![]() $W_{v}$
is the spherical Whittaker function and is normalised so that
$W_{v}$
is the spherical Whittaker function and is normalised so that
where dy is the normal Lebesgue measure.
We turn towards the finite places
![]() $v\neq p$
given by some prime
$v\neq p$
given by some prime
![]() $l\neq p$
. The spherical Whittaker function in
$l\neq p$
. The spherical Whittaker function in
![]() $\mathcal{W}(\pi_v,\psi_v)$
is then given by
$\mathcal{W}(\pi_v,\psi_v)$
is then given by
Here
![]() $\lambda_{\pi}(n)$
is defined by
$\lambda_{\pi}(n)$
is defined by
in analytic normalisation. We have set things up so that
![]() $W_v(1)=1$
.
$W_v(1)=1$
.
Finally we turn towards
![]() $v=p$
. Here we write
$v=p$
. Here we write
![]() $W_p^{(i)}$
for an element in the image of
$W_p^{(i)}$
for an element in the image of
![]() $\mathbb{C} \phi_p^{(i)}$
in the Whittaker model
$\mathbb{C} \phi_p^{(i)}$
in the Whittaker model
![]() $\mathcal{W}(\pi_p,\psi_p)$
such that
$\mathcal{W}(\pi_p,\psi_p)$
such that
here dy is the Haar measure of
![]() $\mathbb{Q}_p$
normalised so that
$\mathbb{Q}_p$
normalised so that
![]() $\operatorname{Vol}(\mathbb{Z}_p,dy)=1$
.
$\operatorname{Vol}(\mathbb{Z}_p,dy)=1$
.
With these choices made there are constants
![]() $C_{\pi}^{(i)}\in \mathbb{C}^{\times}$
so that
$C_{\pi}^{(i)}\in \mathbb{C}^{\times}$
so that
As shown in [ Reference Michel and Venkatesh19 , (4·16)] (see also [ Reference Lapid and Mao16 , section 4]) the absolute values of these constants satisfy
Note that we choose the global measure on
![]() $Z(\mathbb{A})G(\mathbb{Q})\backslash G(\mathbb{A})$
to be the Tamagawa measure. In particular, the absolute value is independent of i and using [
Reference Hoffstein and Lockhart12
] we get
$Z(\mathbb{A})G(\mathbb{Q})\backslash G(\mathbb{A})$
to be the Tamagawa measure. In particular, the absolute value is independent of i and using [
Reference Hoffstein and Lockhart12
] we get
Combining everything we end up with
 \begin{multline} \frac{\phi_i(n(x)a(y))}{\Vert \phi_i\Vert_2} = C_{\pi}^{(i)} \sum_{k\in \mathbb{N}_0}\sum_{\substack{ 0 \neq n\in\mathbb{Z},\\ (n,p)=1}}\operatorname{sgn}(n)^{\rho}\frac{\lambda_{\pi}\left(n\right)}{\sqrt{\lvert{n}\rvert}}W_p^{(i)}(a(np^{k-m_{\pi}})) \\ \cdot W_{\infty}\left(a\left(\frac{n}{p^{m_{\pi}-k}}y\right)\right)e\left(\frac{n}{p^{m_{\pi}-k}}x\right), \nonumber\end{multline}
\begin{multline} \frac{\phi_i(n(x)a(y))}{\Vert \phi_i\Vert_2} = C_{\pi}^{(i)} \sum_{k\in \mathbb{N}_0}\sum_{\substack{ 0 \neq n\in\mathbb{Z},\\ (n,p)=1}}\operatorname{sgn}(n)^{\rho}\frac{\lambda_{\pi}\left(n\right)}{\sqrt{\lvert{n}\rvert}}W_p^{(i)}(a(np^{k-m_{\pi}})) \\ \cdot W_{\infty}\left(a\left(\frac{n}{p^{m_{\pi}-k}}y\right)\right)e\left(\frac{n}{p^{m_{\pi}-k}}x\right), \nonumber\end{multline}
for
![]() $x\in \mathbb{R}$
and
$x\in \mathbb{R}$
and
![]() $y\in \mathbb{R}^+$
. Here
$y\in \mathbb{R}^+$
. Here
![]() $\rho\in\{0,1\}$
depends on whether
$\rho\in\{0,1\}$
depends on whether
![]() $\phi_1,\ldots,\phi_d$
are even or odd.
$\phi_1,\ldots,\phi_d$
are even or odd.
Let
![]() $v_1,\ldots, v_d$
be an orthogonal basis of
$v_1,\ldots, v_d$
be an orthogonal basis of
![]() $\pi_p^{K_p(m_{\pi})}$
. We fix a Whittaker functional and thus an embedding
$\pi_p^{K_p(m_{\pi})}$
. We fix a Whittaker functional and thus an embedding
Define
 \begin{equation} \mathcal{S}_{\pi_p}(g_p) = \sum_{i=1}^d \frac{\lvert{W_{v_i}(g_p)}\rvert^2}{\langle W_{v_i},W_{v_i}\rangle_{\mathcal{W}(\pi_p,\psi_p)}}.\nonumber\end{equation}
\begin{equation} \mathcal{S}_{\pi_p}(g_p) = \sum_{i=1}^d \frac{\lvert{W_{v_i}(g_p)}\rvert^2}{\langle W_{v_i},W_{v_i}\rangle_{\mathcal{W}(\pi_p,\psi_p)}}.\nonumber\end{equation}
Note that
![]() $\mathcal{S}_{\pi_p}$
is well defined as it is independent of the choice of Whittaker functional and the choice of basis
$\mathcal{S}_{\pi_p}$
is well defined as it is independent of the choice of Whittaker functional and the choice of basis
![]() $v_1,\ldots,v_d$
.
$v_1,\ldots,v_d$
.
Lemma 3·1. For any orthonormal basis
![]() $\phi_1,\ldots,\phi_d$
we have
$\phi_1,\ldots,\phi_d$
we have
 \begin{equation} \Phi(g)\leq (dT)^{\epsilon}\sum_{k\in \mathbb{N}_0}\sum_{\substack{ 0 \neq n\in\mathbb{Z},\\ (n,p)=1}}\frac{\lvert{\lambda_{\pi}\left(n\right)}\rvert}{\sqrt{\lvert{n}\rvert}} \cdot \left\lvert{W_{\infty}\left(\frac{n}{p^{m_{\pi}-k}}y\right)}\right\rvert \cdot\mathcal{S}_{\pi_p}(a(np^{k-m_{\pi}}))^{\frac{1}{2}},\nonumber\end{equation}
\begin{equation} \Phi(g)\leq (dT)^{\epsilon}\sum_{k\in \mathbb{N}_0}\sum_{\substack{ 0 \neq n\in\mathbb{Z},\\ (n,p)=1}}\frac{\lvert{\lambda_{\pi}\left(n\right)}\rvert}{\sqrt{\lvert{n}\rvert}} \cdot \left\lvert{W_{\infty}\left(\frac{n}{p^{m_{\pi}-k}}y\right)}\right\rvert \cdot\mathcal{S}_{\pi_p}(a(np^{k-m_{\pi}}))^{\frac{1}{2}},\nonumber\end{equation}
where
![]() $g=n(x)a(y)\in \mathcal{F}$
.
$g=n(x)a(y)\in \mathcal{F}$
.
Proof. To simplify notation we define
if
![]() $t=np^{k-m_{\pi}}$
for
$t=np^{k-m_{\pi}}$
for
![]() $k\in\mathbb{N}_0$
and
$k\in\mathbb{N}_0$
and
![]() $(n,p)=1$
, and
$(n,p)=1$
, and
![]() $a(t)=0=b_i(t)$
otherwise. The Whittaker expansion now neatly reads
$a(t)=0=b_i(t)$
otherwise. The Whittaker expansion now neatly reads
With this at hand we estimate
 \begin{align} \Phi(g) &= \left(\sum_{i=1}^d\left\vert C_{\pi}^{(i)}\sum_{t\in\mathbb{Q}^{\times}}a(t)b_i(t) \right\vert^2\right)^{\frac{1}{2}} \nonumber \\ &\leq\max_i\lvert{C_{\pi}^{(i)}}\rvert\cdot\left(\sum_{t_1\in\mathbb{Q}^{\times}}\sum_{t_2\in\mathbb{Q}^{\times}}a(t_1)\overline{a(t_2)}\sum_{i=1}^d b_i(t_1)\overline{b_i(t_2)}\right)^{\frac{1}{2}} \nonumber \\ & \ll (dT)^{\epsilon} \left(\sum_{t_1\in\mathbb{Q}^{\times}}\sum_{t_2\in\mathbb{Q}^{\times}}\lvert{a(t_1)a(t_2)}\rvert\left(\sum_{i=1}^d\lvert{b_i(t_1)}\rvert^2\right)^{\frac{1}{2}}\left(\sum_{i=1}^d\lvert{b_i(t_2)}\rvert^2\right)^{\frac{1}{2}}\right)^{\frac{1}{2}} \nonumber\\ &=(dT)^{\epsilon}\sum_{t\in\mathbb{Q}^{\times}}\lvert{a(t)}\rvert\left(\sum_{i=1}^d\lvert{b_i(t)}\rvert^2\right)^{\frac{1}{2}}.\nonumber\end{align}
\begin{align} \Phi(g) &= \left(\sum_{i=1}^d\left\vert C_{\pi}^{(i)}\sum_{t\in\mathbb{Q}^{\times}}a(t)b_i(t) \right\vert^2\right)^{\frac{1}{2}} \nonumber \\ &\leq\max_i\lvert{C_{\pi}^{(i)}}\rvert\cdot\left(\sum_{t_1\in\mathbb{Q}^{\times}}\sum_{t_2\in\mathbb{Q}^{\times}}a(t_1)\overline{a(t_2)}\sum_{i=1}^d b_i(t_1)\overline{b_i(t_2)}\right)^{\frac{1}{2}} \nonumber \\ & \ll (dT)^{\epsilon} \left(\sum_{t_1\in\mathbb{Q}^{\times}}\sum_{t_2\in\mathbb{Q}^{\times}}\lvert{a(t_1)a(t_2)}\rvert\left(\sum_{i=1}^d\lvert{b_i(t_1)}\rvert^2\right)^{\frac{1}{2}}\left(\sum_{i=1}^d\lvert{b_i(t_2)}\rvert^2\right)^{\frac{1}{2}}\right)^{\frac{1}{2}} \nonumber\\ &=(dT)^{\epsilon}\sum_{t\in\mathbb{Q}^{\times}}\lvert{a(t)}\rvert\left(\sum_{i=1}^d\lvert{b_i(t)}\rvert^2\right)^{\frac{1}{2}}.\nonumber\end{align}
The claim follows by inserting the definitions of a(t) and
![]() $b_i(t)$
.
$b_i(t)$
.
Before we can estimate this expression we need to investigate the size of the local average
![]() $\mathcal{S}_{\pi_p}(a(y))$
. This is the content of the following subsection.
$\mathcal{S}_{\pi_p}(a(y))$
. This is the content of the following subsection.
3·2. Computing the local averages
The computation of
![]() $\mathcal{S}_{\pi_p}(a(y))$
involves a case study and each case will be treated using different techniques. Finally, combining all possible cases, will lead to the bound
$\mathcal{S}_{\pi_p}(a(y))$
involves a case study and each case will be treated using different techniques. Finally, combining all possible cases, will lead to the bound
See Lemma 3·3, 3·6 and 3·7 below.
3·2·1. The Steinberg representation
Let
![]() $V=\operatorname{Ind}_B^G(\lvert{\cdot}\rvert^{\frac{1}{2}}\otimes \lvert{\cdot}\rvert^{-\frac{1}{2}})$
. Then we can identify
$V=\operatorname{Ind}_B^G(\lvert{\cdot}\rvert^{\frac{1}{2}}\otimes \lvert{\cdot}\rvert^{-\frac{1}{2}})$
. Then we can identify
![]() $\pi=\text{St}$
with the unique irreducible generic subspace of V. Let
$\pi=\text{St}$
with the unique irreducible generic subspace of V. Let
![]() $V^{\vee}=\operatorname{Ind}_B^G(\lvert{\cdot}\rvert^{-\frac{1}{2}}\otimes \lvert{\cdot}\rvert^{\frac{1}{2}})$
. This is the dual space of V and the invariant bilinear pairing is given by
$V^{\vee}=\operatorname{Ind}_B^G(\lvert{\cdot}\rvert^{-\frac{1}{2}}\otimes \lvert{\cdot}\rvert^{\frac{1}{2}})$
. This is the dual space of V and the invariant bilinear pairing is given by
Further
![]() $\tilde{\pi}=\text{St}$
can be identified as the unique irreducible generic sub-quotient of
$\tilde{\pi}=\text{St}$
can be identified as the unique irreducible generic sub-quotient of
![]() $V^{\vee}$
.
$V^{\vee}$
.
Next we choose a basis
![]() $v_0,\ldots,v_p$
of
$v_0,\ldots,v_p$
of
![]() $V^{K_p(1)}$
. (In an analogous way one constructs the dual basis
$V^{K_p(1)}$
. (In an analogous way one constructs the dual basis
![]() $v_0^{\vee},\ldots,v_p^{\vee}$
in
$v_0^{\vee},\ldots,v_p^{\vee}$
in
![]() $(V^{\vee})^{K_p(1)}$
.) This is done as follows: we first construct
$(V^{\vee})^{K_p(1)}$
.) This is done as follows: we first construct
 \begin{equation} v_p(g) = \operatorname{Vol}(B(\mathbb{Z}_p)K_p(1),dk)^{-\frac{1}{2}}\cdot \begin{cases} \displaystyle\lvert{\frac{a}{d}}\rvert &\text{ if }g=\left(\begin{matrix} a&b\\0&d\end{matrix}\right)k\in B(\mathbb{Q}_p)K_p(1),\\ 0&\text{ else.} \end{cases}\nonumber\end{equation}
\begin{equation} v_p(g) = \operatorname{Vol}(B(\mathbb{Z}_p)K_p(1),dk)^{-\frac{1}{2}}\cdot \begin{cases} \displaystyle\lvert{\frac{a}{d}}\rvert &\text{ if }g=\left(\begin{matrix} a&b\\0&d\end{matrix}\right)k\in B(\mathbb{Q}_p)K_p(1),\\ 0&\text{ else.} \end{cases}\nonumber\end{equation}
Further
![]() $\gamma_i=wn(i)$
for
$\gamma_i=wn(i)$
for
![]() $i=0,\ldots,p-1$
. For consistency of the indices we put
$i=0,\ldots,p-1$
. For consistency of the indices we put
![]() $\gamma_p=1$
so that we can identify
$\gamma_p=1$
so that we can identify
via the Bruhat decomposition of
![]() $G(\mathbb{F}_p)$
. (Note that
$G(\mathbb{F}_p)$
. (Note that
![]() $\gamma_0=w$
.) Finally define
$\gamma_0=w$
.) Finally define
![]() $v_i(g) = v_p(g\cdot \gamma_i^{-1})$
. This is the desired basis.
$v_i(g) = v_p(g\cdot \gamma_i^{-1})$
. This is the desired basis.
Now there is an (up to scaling) unique
![]() $\psi_p$
-Whittaker functional
$\psi_p$
-Whittaker functional
![]() $\Lambda\colon V\to \mathbb{C}$
(resp. a unique
$\Lambda\colon V\to \mathbb{C}$
(resp. a unique
![]() $\psi_p^{-1}$
-Whittaker functional
$\psi_p^{-1}$
-Whittaker functional
![]() $\Lambda^{\vee}\colon V^{\vee}\to\mathbb{C}$
). As usual we set
$\Lambda^{\vee}\colon V^{\vee}\to\mathbb{C}$
). As usual we set
We will first consider the related average
 \begin{equation} \mathcal{S}_V(y) = \sum_{i=0}^p W_{v_i}(a(y))W_{v_i^{\vee}}(a(y)). \nonumber\end{equation}
\begin{equation} \mathcal{S}_V(y) = \sum_{i=0}^p W_{v_i}(a(y))W_{v_i^{\vee}}(a(y)). \nonumber\end{equation}
Note that also this is independent of the choice of the particular basis
![]() $v_0,\ldots,v_p$
as long as one considers the corresponding dual basis of
$v_0,\ldots,v_p$
as long as one considers the corresponding dual basis of
![]() $V^{\vee}$
.
$V^{\vee}$
.
We will write
![]() $\int^{st}$
for the stable integral as defined [
Reference Lapid and Mao16
, definition 2·1]. By [
Reference Lapid and Mao16
, lemma 4·4 and remark 4·6] we get
$\int^{st}$
for the stable integral as defined [
Reference Lapid and Mao16
, definition 2·1]. By [
Reference Lapid and Mao16
, lemma 4·4 and remark 4·6] we get
 \begin{align} W_{v_i}(a(y))W_{v_i^{\vee}}(a(y)) &= \int_{\mathbb{Q}_p}^{st}\langle n(x)a(y).v_i,a(y).v_i^{\vee}\rangle\psi_p(x)^{-1}dx\nonumber \\ &= \lvert{y}\rvert_p\int_{\mathbb{Q}_p}^{st}\langle n(x)v_i,v_i^{\vee}\rangle\psi_p(xy)^{-1}dx.\nonumber\end{align}
\begin{align} W_{v_i}(a(y))W_{v_i^{\vee}}(a(y)) &= \int_{\mathbb{Q}_p}^{st}\langle n(x)a(y).v_i,a(y).v_i^{\vee}\rangle\psi_p(x)^{-1}dx\nonumber \\ &= \lvert{y}\rvert_p\int_{\mathbb{Q}_p}^{st}\langle n(x)v_i,v_i^{\vee}\rangle\psi_p(xy)^{-1}dx.\nonumber\end{align}
Knowing the exact shape of the
![]() $v_i$
’s we can compute these integrals. First, we observe that a simple change of variables yields
$v_i$
’s we can compute these integrals. First, we observe that a simple change of variables yields
 \begin{align} \langle n(x).v_i,v_i^{\vee} \rangle &= \int_K v_p(kn(x)\gamma_i^{-1})v_p^{\vee}(k\gamma_i^{-1})dk=\int_K v_p(k\gamma_in(x)\gamma_i^{-1})v_p^{\vee}(k)dk\nonumber\\ &= \frac{\sharp [B(\mathbb{Z}_p)/K_p(1)\cap B(\mathbb{Z}_p)]^{\frac{1}{2}}}{\operatorname{Vol}(K_p(1),dk)^{\frac{1}{2}}}\cdot \int_{K_p(1)} v_p(k\gamma_in(x)\gamma_i^{-1})dk.\nonumber\end{align}
\begin{align} \langle n(x).v_i,v_i^{\vee} \rangle &= \int_K v_p(kn(x)\gamma_i^{-1})v_p^{\vee}(k\gamma_i^{-1})dk=\int_K v_p(k\gamma_in(x)\gamma_i^{-1})v_p^{\vee}(k)dk\nonumber\\ &= \frac{\sharp [B(\mathbb{Z}_p)/K_p(1)\cap B(\mathbb{Z}_p)]^{\frac{1}{2}}}{\operatorname{Vol}(K_p(1),dk)^{\frac{1}{2}}}\cdot \int_{K_p(1)} v_p(k\gamma_in(x)\gamma_i^{-1})dk.\nonumber\end{align}
The case
![]() $i=p$
is somehow special and will be treated later. For now let us assume
$i=p$
is somehow special and will be treated later. For now let us assume
![]() $0\leq i<p$
. In this case we have
$0\leq i<p$
. In this case we have
To take advantage of the support of
![]() $v_p$
we have to investigate
$v_p$
we have to investigate
In view of the Iwahori-factorisation of k we find that
![]() $n(x)\in N(\mathbb{Q}_p)\cap K_p(1)$
is necessary for the integral to be non-zero. Thus one gets
$n(x)\in N(\mathbb{Q}_p)\cap K_p(1)$
is necessary for the integral to be non-zero. Thus one gets
With this at hand it is easy to compute
for
![]() $0\leq i< p$
.
$0\leq i< p$
.
We turn towards
![]() $i=p$
, so that
$i=p$
, so that
![]() $\gamma_p=1$
. Further we replace y by
$\gamma_p=1$
. Further we replace y by
![]() $yp^{-1}$
and consider
$yp^{-1}$
and consider
![]() $y\in\mathbb{Z}_p$
. Recall that every
$y\in\mathbb{Z}_p$
. Recall that every
![]() $k\in K_p(1)$
can be written as
$k\in K_p(1)$
can be written as
![]() $k=t_k\overline{n}_kn_k \in B(\mathbb{Z}_p)N(p\mathbb{Z}_p)^t N(p\mathbb{Z}_p)$
by using the Iwahori-factorisation. We obtain
$k=t_k\overline{n}_kn_k \in B(\mathbb{Z}_p)N(p\mathbb{Z}_p)^t N(p\mathbb{Z}_p)$
by using the Iwahori-factorisation. We obtain
 \begin{align} &\int_{\mathbb{Q}_p}^{st}\langle \pi_p(n(x))v_p,v_p^{\vee}\rangle \psi_p(yp^{-1}x)^{-1}dx \nonumber \\ &\quad = \frac{\sharp [B(\mathbb{Z}_p)/K_p(1)\cap B(\mathbb{Z}_p)]^{\frac{1}{2}}}{\operatorname{Vol}(K_p(1),dk)^{\frac{1}{2}}}\cdot\int_{\mathbb{Q}_p}^{st}\int_{K_p(1)} v_p(kn(x))dk \psi_p(yp^{-1}x)^{-1}dx \nonumber \\ &\quad = \frac{\sharp [B(\mathbb{Z}_p)/K_p(1)\cap B(\mathbb{Z}_p)]^{\frac{1}{2}}}{\operatorname{Vol}(K_p(1),dk)^{\frac{1}{2}}}\cdot \int_{K_p(1)}\int_{\mathbb{Q}_p}^{st} v_p(\overline{n}_kn(x)) \psi_p(yp^{-1}x)^{-1}dxdk.\nonumber\end{align}
\begin{align} &\int_{\mathbb{Q}_p}^{st}\langle \pi_p(n(x))v_p,v_p^{\vee}\rangle \psi_p(yp^{-1}x)^{-1}dx \nonumber \\ &\quad = \frac{\sharp [B(\mathbb{Z}_p)/K_p(1)\cap B(\mathbb{Z}_p)]^{\frac{1}{2}}}{\operatorname{Vol}(K_p(1),dk)^{\frac{1}{2}}}\cdot\int_{\mathbb{Q}_p}^{st}\int_{K_p(1)} v_p(kn(x))dk \psi_p(yp^{-1}x)^{-1}dx \nonumber \\ &\quad = \frac{\sharp [B(\mathbb{Z}_p)/K_p(1)\cap B(\mathbb{Z}_p)]^{\frac{1}{2}}}{\operatorname{Vol}(K_p(1),dk)^{\frac{1}{2}}}\cdot \int_{K_p(1)}\int_{\mathbb{Q}_p}^{st} v_p(\overline{n}_kn(x)) \psi_p(yp^{-1}x)^{-1}dxdk.\nonumber\end{align}
Note that the integrand only depends on
![]() $\overline{n}_k$
. Therefore we start by discussing a suitable measure on
$\overline{n}_k$
. Therefore we start by discussing a suitable measure on
![]() $K_p(1)$
. Indeed using the Iwahori factorisation we can write
$K_p(1)$
. Indeed using the Iwahori factorisation we can write
If we write
![]() $\tilde{v}_p$
to be the re-normalisation of
$\tilde{v}_p$
to be the re-normalisation of
![]() $v_p$
with
$v_p$
with
![]() $\tilde{v}_p(1)=1$
, then we have
$\tilde{v}_p(1)=1$
, then we have
 \begin{align} \int_{\mathbb{Q}_p}^{st}\langle \pi_p(n(x))v_p,v_p^{\vee}\rangle \psi_p(yp^{-1}x)^{-1}dx &= p\int_{\mathbb{Q}_p}^{st}\int_{p\mathbb{Z}_p} \tilde{v}_p(n(z)^tn(x)) \psi_p(yp^{-1}x)^{-1}dzdx \nonumber \\ &{=} p\int_{\mathbb{Q}_p}^{st}\int_{p\mathbb{Z}_p} \!\!\tilde{v}_p\left(\left(\begin{matrix} 1&\!x-z^{-1} \\ z &\! zx\end{matrix}\right)\right) \psi_p(yp^{-1}(x{-}z^{-1}))^{-1}dzdx.\nonumber\end{align}
\begin{align} \int_{\mathbb{Q}_p}^{st}\langle \pi_p(n(x))v_p,v_p^{\vee}\rangle \psi_p(yp^{-1}x)^{-1}dx &= p\int_{\mathbb{Q}_p}^{st}\int_{p\mathbb{Z}_p} \tilde{v}_p(n(z)^tn(x)) \psi_p(yp^{-1}x)^{-1}dzdx \nonumber \\ &{=} p\int_{\mathbb{Q}_p}^{st}\int_{p\mathbb{Z}_p} \!\!\tilde{v}_p\left(\left(\begin{matrix} 1&\!x-z^{-1} \\ z &\! zx\end{matrix}\right)\right) \psi_p(yp^{-1}(x{-}z^{-1}))^{-1}dzdx.\nonumber\end{align}
In the last step we simply made a change of variables in the x-integral. A simple matrix computation shows that
Inserting this and using the transformation behaviour of
![]() $\tilde{v}_p$
one obtains
$\tilde{v}_p$
one obtains
 \begin{multline} \int_{\mathbb{Q}_p}^{st}\langle \pi_p(n(x))v_p,v_p^{\vee}\rangle \psi_p(yp^{-1}x)^{-1}dx \\ = p\int_{p\mathbb{Z}_p}\psi_p(yz^{-1}p^{-1})\frac{dz}{\lvert{z}\rvert_p^2}\int_{\mathbb{Q}_p}^{st}\tilde{v}_p\left(\left(\begin{matrix} 1& 0\\x^{-1} & 1 \end{matrix}\right)\right)\psi_p(\!-xyp^{-1})\frac{dx}{\lvert{x}\rvert_p^2}.\nonumber\end{multline}
\begin{multline} \int_{\mathbb{Q}_p}^{st}\langle \pi_p(n(x))v_p,v_p^{\vee}\rangle \psi_p(yp^{-1}x)^{-1}dx \\ = p\int_{p\mathbb{Z}_p}\psi_p(yz^{-1}p^{-1})\frac{dz}{\lvert{z}\rvert_p^2}\int_{\mathbb{Q}_p}^{st}\tilde{v}_p\left(\left(\begin{matrix} 1& 0\\x^{-1} & 1 \end{matrix}\right)\right)\psi_p(\!-xyp^{-1})\frac{dx}{\lvert{x}\rvert_p^2}.\nonumber\end{multline}
Both integrals can now be computed quite easily. Starting from the first one we obtain
 \begin{multline} p\int_{p\mathbb{Z}_p}\psi_p(yz^{-1}p^{-1})\frac{dz}{\lvert{z}\rvert_p^2} = \sum_{l=1}^{\infty}p^{l+1}\int_{\mathbb{Z}_p^{\times}}\psi_p(zyp^{-1-l})dz \nonumber \\ = \sum_{l=1}^{v_p(y)-1}p^{l+1}(1-p^{-1})-\delta_{v_p(y)\geq 1}p^{v_p(y)} = -p\delta_{v_p(y)\geq 1}.\nonumber\end{multline}
\begin{multline} p\int_{p\mathbb{Z}_p}\psi_p(yz^{-1}p^{-1})\frac{dz}{\lvert{z}\rvert_p^2} = \sum_{l=1}^{\infty}p^{l+1}\int_{\mathbb{Z}_p^{\times}}\psi_p(zyp^{-1-l})dz \nonumber \\ = \sum_{l=1}^{v_p(y)-1}p^{l+1}(1-p^{-1})-\delta_{v_p(y)\geq 1}p^{v_p(y)} = -p\delta_{v_p(y)\geq 1}.\nonumber\end{multline}
Turning to the other integral we find
 \begin{align} \int_{\mathbb{Q}_p}^{st}\tilde{v}_p\left(\left(\begin{matrix} 1& 0\\x^{-1} & 1 \end{matrix}\right)\right)\psi_p(\!-xyp^{-1})\frac{dx}{\lvert{x}\rvert_p^2} &= \int_{\mathbb{Q}_p\setminus \mathbb{Z}_p}^{st}\psi_p(\!-xyp^{-1})\frac{dx}{\lvert{x}\rvert_p^2} \nonumber \\ &= \sum_{l=1}^{\infty}p^{-l}\int_{\mathbb{Z}_p^{\times}}\psi_p(\!-xyp^{-1-l})dx \nonumber\\ &= \sum_{l=1}^{v_p(y)-1}p^{-l}(1-p^{-1})-\delta_{v_p(y)\geq 1}p^{-v_p(y)-1} \nonumber \\ &= \delta_{v_p(y)\geq 2}(p^{-1}-p^{-v_p(y)})-\delta_{v_p(y)\geq 1}p^{-1-v_p(y)}.\nonumber\end{align}
\begin{align} \int_{\mathbb{Q}_p}^{st}\tilde{v}_p\left(\left(\begin{matrix} 1& 0\\x^{-1} & 1 \end{matrix}\right)\right)\psi_p(\!-xyp^{-1})\frac{dx}{\lvert{x}\rvert_p^2} &= \int_{\mathbb{Q}_p\setminus \mathbb{Z}_p}^{st}\psi_p(\!-xyp^{-1})\frac{dx}{\lvert{x}\rvert_p^2} \nonumber \\ &= \sum_{l=1}^{\infty}p^{-l}\int_{\mathbb{Z}_p^{\times}}\psi_p(\!-xyp^{-1-l})dx \nonumber\\ &= \sum_{l=1}^{v_p(y)-1}p^{-l}(1-p^{-1})-\delta_{v_p(y)\geq 1}p^{-v_p(y)-1} \nonumber \\ &= \delta_{v_p(y)\geq 2}(p^{-1}-p^{-v_p(y)})-\delta_{v_p(y)\geq 1}p^{-1-v_p(y)}.\nonumber\end{align}
In particular we have
Note that this can be negative, but for non-unitary representations there is no expectation for these integrals to be non-negative.
Combining the computations above and swapping back to
![]() $y\in p^{-1}\mathbb{Z}_p$
leads us to the following result.
$y\in p^{-1}\mathbb{Z}_p$
leads us to the following result.
Lemma 3·2. In the notation above we have
We will obtain the desired estimate by relating
![]() $\mathcal{S}_{\text{St}}(a(y))$
to
$\mathcal{S}_{\text{St}}(a(y))$
to
![]() $\mathcal{S}_V$
.
$\mathcal{S}_V$
.
Lemma 3·3. For
![]() $\pi_p=\text{St}$
and
$\pi_p=\text{St}$
and
![]() $y\in \mathbb{Q}_p$
we have
$y\in \mathbb{Q}_p$
we have
Proof. Recall that the definitions of
![]() $\mathcal{S}_{\pi_p}$
and
$\mathcal{S}_{\pi_p}$
and
![]() $\mathcal{S}_V$
are independent of the choice of the underlying basis. Thus we can choose an orthogonal basis
$\mathcal{S}_V$
are independent of the choice of the underlying basis. Thus we can choose an orthogonal basis
![]() $w_1,\ldots,w_p$
of
$w_1,\ldots,w_p$
of
![]() $\pi_p^{K_p(1)}$
. Viewing
$\pi_p^{K_p(1)}$
. Viewing
![]() $\pi$
as invariant subspace of V we can assume that the
$\pi$
as invariant subspace of V we can assume that the
![]() $w_i$
’s are in V. We then have
$w_i$
’s are in V. We then have
 \begin{equation} \mathcal{S}_{\pi}(a(y)) = \sum_{i=1}^p \frac{\lvert{W_{w_i}(a(y))}\rvert^2}{\langle W_{w_i},W_{w_i}\rangle} = \sum_{i=1}^p \frac{W_{w_i}(a(y))W_{w_i^{\vee}}(a(y))}{\langle w_i,w_i^{\vee}\rangle}. \nonumber\end{equation}
\begin{equation} \mathcal{S}_{\pi}(a(y)) = \sum_{i=1}^p \frac{\lvert{W_{w_i}(a(y))}\rvert^2}{\langle W_{w_i},W_{w_i}\rangle} = \sum_{i=1}^p \frac{W_{w_i}(a(y))W_{w_i^{\vee}}(a(y))}{\langle w_i,w_i^{\vee}\rangle}. \nonumber\end{equation}
Finally if we choose
![]() $w_0^{\vee}\in (V^{\vee})^{K_p(1)}$
in the annihilator of the
$w_0^{\vee}\in (V^{\vee})^{K_p(1)}$
in the annihilator of the
![]() $w_1,\ldots,w_p$
and let
$w_1,\ldots,w_p$
and let
![]() $w_0\in V^{K_p(1)}$
be the dual element then after renormalising we have
$w_0\in V^{K_p(1)}$
be the dual element then after renormalising we have
However, since there is a unique Whittaker functional on
![]() $V^{\vee}$
which descents to the unique Whittaker functional on
$V^{\vee}$
which descents to the unique Whittaker functional on
![]() $\pi$
when viewed as a sub-quotient we must have
$\pi$
when viewed as a sub-quotient we must have
![]() $W_{w_0^{\vee}}(a(y))=0$
. (Since the unique invariant subspace is non-generic.) Thus
$W_{w_0^{\vee}}(a(y))=0$
. (Since the unique invariant subspace is non-generic.) Thus
![]() $\mathcal{S}_V(y) = \mathcal{S}_{\pi_p}(a(y))$
and the desired estimate follows directly from the previous lemma.
$\mathcal{S}_V(y) = \mathcal{S}_{\pi_p}(a(y))$
and the desired estimate follows directly from the previous lemma.
3·2·2. Twist minimal principal series
Turning to this case we assume that
![]() $\pi_p=\chi \cdot \lvert{\cdot}\rvert^{\rho}\boxplus \lvert{\cdot}\rvert^{-\rho}$
where
$\pi_p=\chi \cdot \lvert{\cdot}\rvert^{\rho}\boxplus \lvert{\cdot}\rvert^{-\rho}$
where
![]() $a(\chi)=n_{\pi}>0$
. Without loss of generality we can assume that
$a(\chi)=n_{\pi}>0$
. Without loss of generality we can assume that
![]() $\chi(p)=1$
. (If we assume that
$\chi(p)=1$
. (If we assume that
![]() $\pi$
is unitary then it is tempered so that
$\pi$
is unitary then it is tempered so that
![]() $\rho\in i\mathbb{R}$
.) Now we can choose a basis in the induced picture essentially as above, but we need to find a suitable decomposition of
$\rho\in i\mathbb{R}$
.) Now we can choose a basis in the induced picture essentially as above, but we need to find a suitable decomposition of
![]() $B(\mathbb{Z}_p)\backslash K_p/K_p(n_{\pi})$
(since the Bruhat decomposition does not hold in
$B(\mathbb{Z}_p)\backslash K_p/K_p(n_{\pi})$
(since the Bruhat decomposition does not hold in
![]() $G(\mathbb{Z}_p/p^m\mathbb{Z}_p)$
if
$G(\mathbb{Z}_p/p^m\mathbb{Z}_p)$
if
![]() $m>1$
). First we start by defining
$m>1$
). First we start by defining
 \begin{equation} v_0(g) = \operatorname{Vol}(B(\mathbb{Z}_p)K_p(m_{\pi}),dk)^{-\frac{1}{2}}\cdot \begin{cases} \chi(a)\lvert{\frac{a}{d}}\rvert^{\frac{1}{2}+\rho} &\text{ if }g=\left(\begin{matrix} a&b\\0&d\end{matrix}\right)k\in B(\mathbb{Q}_p)K_p(m_{\pi}),\\ 0&\text{ else.}\end{cases}\nonumber\end{equation}
\begin{equation} v_0(g) = \operatorname{Vol}(B(\mathbb{Z}_p)K_p(m_{\pi}),dk)^{-\frac{1}{2}}\cdot \begin{cases} \chi(a)\lvert{\frac{a}{d}}\rvert^{\frac{1}{2}+\rho} &\text{ if }g=\left(\begin{matrix} a&b\\0&d\end{matrix}\right)k\in B(\mathbb{Q}_p)K_p(m_{\pi}),\\ 0&\text{ else.}\end{cases}\nonumber\end{equation}
From this element we can construct a basis of
![]() $\pi_p^{K_p(m_{\pi})}$
as in the Steinberg case. Indeed, we fix a system of representatives
$\pi_p^{K_p(m_{\pi})}$
as in the Steinberg case. Indeed, we fix a system of representatives
![]() $\{\gamma_j\}$
for
$\{\gamma_j\}$
for
![]() $B(\mathbb{Z}_p)\backslash K_p/K_p(m_{\pi})$
and set
$B(\mathbb{Z}_p)\backslash K_p/K_p(m_{\pi})$
and set
![]() $v_j=\pi_p(\gamma_j^{-1})v_0$
.
$v_j=\pi_p(\gamma_j^{-1})v_0$
.
In order to explicate this basis we need to compute a suitable coset decomposition for
![]() $B(\mathbb{Z}_p)\backslash K_p/K_p(m_{\pi})$
. This is the content of the following lemma.
$B(\mathbb{Z}_p)\backslash K_p/K_p(m_{\pi})$
. This is the content of the following lemma.
Lemma 3·4. We have
 \begin{equation} K_p = \bigsqcup_{a\in \mathbb{Z}_p/p^{m_{\pi}}\mathbb{Z}_p} B(\mathbb{Z}_p) \gamma_{0,a} K_p(m_{\pi}) \sqcup \bigsqcup_{i=1}^{m_{\pi}}\bigsqcup_{a\in (\mathbb{Z}_p/p^{m_{\pi}-i}\mathbb{Z}_p)^{\times}} B(\mathbb{Z}_p)\gamma_{i,a} K_p(m_{\pi}),\nonumber\end{equation}
\begin{equation} K_p = \bigsqcup_{a\in \mathbb{Z}_p/p^{m_{\pi}}\mathbb{Z}_p} B(\mathbb{Z}_p) \gamma_{0,a} K_p(m_{\pi}) \sqcup \bigsqcup_{i=1}^{m_{\pi}}\bigsqcup_{a\in (\mathbb{Z}_p/p^{m_{\pi}-i}\mathbb{Z}_p)^{\times}} B(\mathbb{Z}_p)\gamma_{i,a} K_p(m_{\pi}),\nonumber\end{equation}
for
 \begin{equation} \gamma_{i,a} = \begin{cases} \left(\begin{matrix} 0& -1 \\ 1 & a\end{matrix} \right) & \text{ if }i=0,\\ \left(\begin{matrix} 1 & 0 \\ ap^i &1 \end{matrix} \right) &\text{ if } 1\leq i\leq m_{\pi}-1, \\ 1_2 &\text{ if }i=m_{\pi}. \end{cases} \nonumber\end{equation}
\begin{equation} \gamma_{i,a} = \begin{cases} \left(\begin{matrix} 0& -1 \\ 1 & a\end{matrix} \right) & \text{ if }i=0,\\ \left(\begin{matrix} 1 & 0 \\ ap^i &1 \end{matrix} \right) &\text{ if } 1\leq i\leq m_{\pi}-1, \\ 1_2 &\text{ if }i=m_{\pi}. \end{cases} \nonumber\end{equation}
Proof. Take
![]() $g=\left(\begin{matrix} a&b\\c & d\end{matrix}\right)\in K_p$
and set
$g=\left(\begin{matrix} a&b\\c & d\end{matrix}\right)\in K_p$
and set
![]() $i=v_p(c)$
. We treat several cases distinguished by the value of i.
$i=v_p(c)$
. We treat several cases distinguished by the value of i.
First, if
![]() $i=m_{\pi}$
, then we have
$i=m_{\pi}$
, then we have
Second, for
![]() $1\leq i<m_{\pi}$
we have
$1\leq i<m_{\pi}$
we have
By right multiplication with elements in
![]() $K_p(m_{\pi})$
we can view
$K_p(m_{\pi})$
we can view
![]() ${c}/{d} \in p^i\mathbb{Z}_p^{\times}/p^{m_{\pi}}\mathbb{Z}_p$
.
${c}/{d} \in p^i\mathbb{Z}_p^{\times}/p^{m_{\pi}}\mathbb{Z}_p$
.
The critical contribution is given by the matrices with
![]() $i=0$
. We can write
$i=0$
. We can write
 \begin{equation} g= \left(\begin{matrix} \frac{ad}{c}-b & a+(b-\frac{ad}{c})p^{m_{\pi}}\\ 0 & c \end{matrix}\right)\left(\begin{matrix}0 & -1 \\ 1 & \frac{d}{c} \end{matrix}\right)\left(\begin{matrix} 1+\frac{d}{c}p^{m_{\pi}} & \frac{d^2}{c^2}p^{m_{\pi}} \\ -p^{m_{\pi}} & 1-\frac{d}{c}p^{m_{\pi}} \end{matrix}\right). \nonumber\end{equation}
\begin{equation} g= \left(\begin{matrix} \frac{ad}{c}-b & a+(b-\frac{ad}{c})p^{m_{\pi}}\\ 0 & c \end{matrix}\right)\left(\begin{matrix}0 & -1 \\ 1 & \frac{d}{c} \end{matrix}\right)\left(\begin{matrix} 1+\frac{d}{c}p^{m_{\pi}} & \frac{d^2}{c^2}p^{m_{\pi}} \\ -p^{m_{\pi}} & 1-\frac{d}{c}p^{m_{\pi}} \end{matrix}\right). \nonumber\end{equation}
Given
![]() $v \in \pi^{K_p(n_{\pi})}$
we can compute the Jacquet Integral as follows. Without loss of generality assume
$v \in \pi^{K_p(n_{\pi})}$
we can compute the Jacquet Integral as follows. Without loss of generality assume
![]() $v_p(y)\geq -n_{\pi}$
, since otherwise the Whittaker function
$v_p(y)\geq -n_{\pi}$
, since otherwise the Whittaker function
![]() $W_v$
vanishes for trivial reasons. We compute
$W_v$
vanishes for trivial reasons. We compute
 \begin{align} W_v(a(y)) &= \int_{\mathbb{Q}_p} v(wn(x)a(y))\psi_p(x)^{-1}dx \nonumber \\ &= \lvert{y}\rvert_p^{\frac{1}{2}-\rho}\int_{\mathbb{Q}_p}v(wn(x))\psi_p(xy)^{-1}dx\nonumber \\ &= \lvert{y}\rvert_p^{\frac{1}{2}-\rho} p^{-n_{\pi}}\sum_{a\in \mathbb{Z}_p/p^{n_{\pi}}\mathbb{Z}_p} \psi_p(ay)^{-1}v(wn(a)) \nonumber \\ &\qquad + \lvert{y}\rvert_p^{\frac{1}{2}-\rho}\int_{\mathbb{Q}_p\setminus \mathbb{Z}_p}\lvert{x}\rvert^{-2\rho} \chi(x)^{-1}\psi(xy)^{-1}v(n(x^{-1})^t)\frac{dx}{\lvert{x}\rvert_p}.\nonumber\end{align}
\begin{align} W_v(a(y)) &= \int_{\mathbb{Q}_p} v(wn(x)a(y))\psi_p(x)^{-1}dx \nonumber \\ &= \lvert{y}\rvert_p^{\frac{1}{2}-\rho}\int_{\mathbb{Q}_p}v(wn(x))\psi_p(xy)^{-1}dx\nonumber \\ &= \lvert{y}\rvert_p^{\frac{1}{2}-\rho} p^{-n_{\pi}}\sum_{a\in \mathbb{Z}_p/p^{n_{\pi}}\mathbb{Z}_p} \psi_p(ay)^{-1}v(wn(a)) \nonumber \\ &\qquad + \lvert{y}\rvert_p^{\frac{1}{2}-\rho}\int_{\mathbb{Q}_p\setminus \mathbb{Z}_p}\lvert{x}\rvert^{-2\rho} \chi(x)^{-1}\psi(xy)^{-1}v(n(x^{-1})^t)\frac{dx}{\lvert{x}\rvert_p}.\nonumber\end{align}
Note that
![]() $wn(a) = \gamma_{0,a}$
. Now we will have a closer look at the remaining integral:
$wn(a) = \gamma_{0,a}$
. Now we will have a closer look at the remaining integral:
 \begin{align} &\int_{\mathbb{Q}_p\setminus \mathbb{Z}_p}\lvert{x}\rvert^{-2\rho} \chi(x)^{-1}\psi(xy)^{-1}v(n(x^{-1})^t)\frac{dx}{\lvert{x}\rvert_p} \nonumber \\ &\qquad = \int_{p\mathbb{Z}_p}\lvert{x}\rvert^{2\rho} \chi(x)\psi(x^{-1}y)^{-1}v(n(x)^t)\frac{dx}{\lvert{x}\rvert_p} \nonumber\\ &\qquad = v(1)\int_{p^{m_{\pi}}\mathbb{Z}_p}\chi(x)\lvert{x}\rvert^{2\rho}\psi(x^{-1}y)^{-1}\frac{dx}{\lvert{x}\rvert_p} \nonumber \\ &\qquad\qquad +\sum_{i=1}^{m_{\pi}-1}\sum_{b\in (\mathbb{Z}_p/p^{m_{\pi}-i}\mathbb{Z}_p)^{\times}}p^{-2\rho i}\chi(b)^{-1}v(n(bp^i)^t)\cdot \int_{1+p^{m_{\pi}-i}\mathbb{Z}_p}\chi(x)^{-1}\psi(\!-byxp^{-i})dx.\nonumber\end{align}
\begin{align} &\int_{\mathbb{Q}_p\setminus \mathbb{Z}_p}\lvert{x}\rvert^{-2\rho} \chi(x)^{-1}\psi(xy)^{-1}v(n(x^{-1})^t)\frac{dx}{\lvert{x}\rvert_p} \nonumber \\ &\qquad = \int_{p\mathbb{Z}_p}\lvert{x}\rvert^{2\rho} \chi(x)\psi(x^{-1}y)^{-1}v(n(x)^t)\frac{dx}{\lvert{x}\rvert_p} \nonumber\\ &\qquad = v(1)\int_{p^{m_{\pi}}\mathbb{Z}_p}\chi(x)\lvert{x}\rvert^{2\rho}\psi(x^{-1}y)^{-1}\frac{dx}{\lvert{x}\rvert_p} \nonumber \\ &\qquad\qquad +\sum_{i=1}^{m_{\pi}-1}\sum_{b\in (\mathbb{Z}_p/p^{m_{\pi}-i}\mathbb{Z}_p)^{\times}}p^{-2\rho i}\chi(b)^{-1}v(n(bp^i)^t)\cdot \int_{1+p^{m_{\pi}-i}\mathbb{Z}_p}\chi(x)^{-1}\psi(\!-byxp^{-i})dx.\nonumber\end{align}
Note that
![]() $n(bp^i)^t=\gamma_{i,b}$
.
$n(bp^i)^t=\gamma_{i,b}$
.
Since the v(1)-contribution is easily computed we arrive at the following lemma.
Lemma 3·5. For
![]() $v_p(y)\geq -m_{\pi}$
we have
$v_p(y)\geq -m_{\pi}$
we have
 \begin{align} W_v(a(y)) &= \lvert{y}\rvert_p^{\frac{1}{2}-\rho}p^{-m_{\pi}}\sum_{a\in \mathbb{Z}_p/p^{m_{\pi}}\mathbb{Z}_p}\psi_p(ay)^{-1}v(\gamma_{0,a}) \nonumber \\ &\qquad + \lvert{y}\rvert_p^{\frac{1}{2}-\rho}\sum_{i=1}^{m_{\pi}-1}\sum_{b\in (\mathbb{Z}_p/p^{m_{\pi}-i}\mathbb{Z}_p)^{\times}}p^{-2\rho i}\chi(b)^{-1}v(\gamma_{i,b})G_{m_{\pi}-i}(\!-byp^{-i},\chi^{-1}) \nonumber\\ &\qquad +\lvert{y}\rvert_p^{\frac{1}{2}-\rho}\cdot v(\gamma_{m_{\pi},0})\cdot \int_{p^{m_{\pi}}\mathbb{Z}_p}\chi(x)\lvert{x}\rvert^{2\rho}\psi(x^{-1}y)^{-1}\frac{dx}{\lvert{x}\rvert_p}, \nonumber\end{align}
\begin{align} W_v(a(y)) &= \lvert{y}\rvert_p^{\frac{1}{2}-\rho}p^{-m_{\pi}}\sum_{a\in \mathbb{Z}_p/p^{m_{\pi}}\mathbb{Z}_p}\psi_p(ay)^{-1}v(\gamma_{0,a}) \nonumber \\ &\qquad + \lvert{y}\rvert_p^{\frac{1}{2}-\rho}\sum_{i=1}^{m_{\pi}-1}\sum_{b\in (\mathbb{Z}_p/p^{m_{\pi}-i}\mathbb{Z}_p)^{\times}}p^{-2\rho i}\chi(b)^{-1}v(\gamma_{i,b})G_{m_{\pi}-i}(\!-byp^{-i},\chi^{-1}) \nonumber\\ &\qquad +\lvert{y}\rvert_p^{\frac{1}{2}-\rho}\cdot v(\gamma_{m_{\pi},0})\cdot \int_{p^{m_{\pi}}\mathbb{Z}_p}\chi(x)\lvert{x}\rvert^{2\rho}\psi(x^{-1}y)^{-1}\frac{dx}{\lvert{x}\rvert_p}, \nonumber\end{align}
for
This supplies us with the necessary ingredients to show the required estimate for
![]() $\mathcal{S}_{\pi_p}$
.
$\mathcal{S}_{\pi_p}$
.
Lemma 3·6. For
![]() $\pi_p=\chi\lvert{\cdot}\rvert^{\rho}\boxplus \lvert{\cdot}\rvert^{-\rho}$
unitary and
$\pi_p=\chi\lvert{\cdot}\rvert^{\rho}\boxplus \lvert{\cdot}\rvert^{-\rho}$
unitary and
![]() $y\in \mathbb{Q}_p$
we have
$y\in \mathbb{Q}_p$
we have
Proof. Note that since all
![]() $v_j$
’s are translates of
$v_j$
’s are translates of
![]() $v_0$
their Whittaker-norm all coincides. So it suffices to compute one of these norms and it is easy to see that
$v_0$
their Whittaker-norm all coincides. So it suffices to compute one of these norms and it is easy to see that
Next we observe that one can choose representatives so that
![]() $v_j=\pi_p(\gamma_{i,a}^{-1})v_0$
for some
$v_j=\pi_p(\gamma_{i,a}^{-1})v_0$
for some
![]() $i=i(j)$
and
$i=i(j)$
and
![]() $a=a(j)$
. In particular, we can sort the terms of the sum
$a=a(j)$
. In particular, we can sort the terms of the sum
![]() $\mathcal{S}_{\pi_p}(a(y))$
according to this i. We get
$\mathcal{S}_{\pi_p}(a(y))$
according to this i. We get
 \begin{equation} \mathcal{S}_{\pi_p}(a(y)) = \sum_{i=0}^{m_{\pi}} \mathcal{S}_i(y) \text{ for } \mathcal{S}_i(y) = (1+p^{-1})^{-1}\sum_{a\in \mathbb{Z}_p/p^{m_{\pi}-i}\mathbb{Z}_p} \lvert{W_{\pi_p(\gamma_{i,a}^{-1})v_0}(a(y))}\rvert^2.\nonumber\end{equation}
\begin{equation} \mathcal{S}_{\pi_p}(a(y)) = \sum_{i=0}^{m_{\pi}} \mathcal{S}_i(y) \text{ for } \mathcal{S}_i(y) = (1+p^{-1})^{-1}\sum_{a\in \mathbb{Z}_p/p^{m_{\pi}-i}\mathbb{Z}_p} \lvert{W_{\pi_p(\gamma_{i,a}^{-1})v_0}(a(y))}\rvert^2.\nonumber\end{equation}
Applying the previous Lemma with
![]() $v=\pi_p(\gamma_{i,a}^{-1})v_0$
and taking support properties of
$v=\pi_p(\gamma_{i,a}^{-1})v_0$
and taking support properties of
![]() $v_0$
into account provides us with nice formulae for the
$v_0$
into account provides us with nice formulae for the
![]() $W_{\pi_p(\gamma_{i,a}^{-1})v_0}(a(y))$
.
$W_{\pi_p(\gamma_{i,a}^{-1})v_0}(a(y))$
.
As soon as we can show that
![]() $\mathcal{S}_i(y)\ll \lvert{y}\rvert_p$
for all i we are done. We start with
$\mathcal{S}_i(y)\ll \lvert{y}\rvert_p$
for all i we are done. We start with
![]() $i=0$
. Here we have the explicit formula
$i=0$
. Here we have the explicit formula
 \begin{equation} \mathcal{S}_i(y) = (1+p^{-1})^{-1}\sum_{a\in \mathbb{Z}_p/p^{m_{\pi}}\mathbb{Z}_p} p^{-2m_{\pi}}\lvert{y}\rvert_p v_0(1)^2 = \frac{(1+p^{-1})^{-1}p^{-m_{\pi}}\lvert{y}\rvert_p}{ \operatorname{Vol}(B(\mathbb{Z}_p)K_p(m_{\pi}),dk)} = \lvert{y}\rvert_p\nonumber\end{equation}
\begin{equation} \mathcal{S}_i(y) = (1+p^{-1})^{-1}\sum_{a\in \mathbb{Z}_p/p^{m_{\pi}}\mathbb{Z}_p} p^{-2m_{\pi}}\lvert{y}\rvert_p v_0(1)^2 = \frac{(1+p^{-1})^{-1}p^{-m_{\pi}}\lvert{y}\rvert_p}{ \operatorname{Vol}(B(\mathbb{Z}_p)K_p(m_{\pi}),dk)} = \lvert{y}\rvert_p\nonumber\end{equation}
for
![]() $y\in p^{-m_{\pi}}\mathbb{Z}_p$
.
$y\in p^{-m_{\pi}}\mathbb{Z}_p$
.
We turn towards
![]() $1\leq i \leq m_{\pi}-1$
. In this range we get
$1\leq i \leq m_{\pi}-1$
. In this range we get
Thus we need to bound the integrals
![]() $G_l(z,\chi)$
, which are somehow incomplete Gauß sums in the sense that one sums only over a specific congruence class. These sums were essentially computed in the proof of [
Reference Assing2
, lemma 5·8]. Indeed one extracts
$G_l(z,\chi)$
, which are somehow incomplete Gauß sums in the sense that one sums only over a specific congruence class. These sums were essentially computed in the proof of [
Reference Assing2
, lemma 5·8]. Indeed one extracts
 \begin{equation} G_l(zp^{-k},\chi) = \begin{cases} \epsilon(\frac{1}{2},\chi^{-1})\chi^{-1}(z)p^{-\frac{k}{2}} &\text{ if }l\leq \lfloor \frac{a(\chi)}{2}\rfloor, k=a(\chi) \text{ and }z\in b(\chi)+p^l\mathbb{Z}_p,\\ \psi_p(zp^k)p^{-l} &\text{ if }l\geq \lceil \frac{a(\chi)}{2}\rceil, k=a(\chi) \text{ and }z\in -b(\chi)+p^{a(\chi)-l}\mathbb{Z}_p,\\ 0&\text{ else}, \end{cases} \nonumber\end{equation}
\begin{equation} G_l(zp^{-k},\chi) = \begin{cases} \epsilon(\frac{1}{2},\chi^{-1})\chi^{-1}(z)p^{-\frac{k}{2}} &\text{ if }l\leq \lfloor \frac{a(\chi)}{2}\rfloor, k=a(\chi) \text{ and }z\in b(\chi)+p^l\mathbb{Z}_p,\\ \psi_p(zp^k)p^{-l} &\text{ if }l\geq \lceil \frac{a(\chi)}{2}\rceil, k=a(\chi) \text{ and }z\in -b(\chi)+p^{a(\chi)-l}\mathbb{Z}_p,\\ 0&\text{ else}, \end{cases} \nonumber\end{equation}
for
![]() $z\in \mathbb{Z}_p^{\times}$
,
$z\in \mathbb{Z}_p^{\times}$
,
![]() $k\in \mathbb{Z}$
and
$k\in \mathbb{Z}$
and
![]() $b(\chi)\in \mathbb{Z}_p^{\times}$
is determined by
$b(\chi)\in \mathbb{Z}_p^{\times}$
is determined by
![]() $\chi$
. With this at hand we can easily evaluate
$\chi$
. With this at hand we can easily evaluate
![]() $\mathcal{S}_i$
. For
$\mathcal{S}_i$
. For
![]() $i\leq \lfloor {m_{\pi}}/{2}\rfloor$
we have
$i\leq \lfloor {m_{\pi}}/{2}\rfloor$
we have
 \begin{align} \mathcal{S}_i(y) &= \delta_{v_p(y) =i-m_{\pi}}(1+p^{-1})^{-1}v_0(1)^2\lvert{y}\rvert_p \sum_{b\in (\mathbb{Z}_p/p^{m_{\pi}-i}\mathbb{Z}_p)^{\times}}p^{2i-2m_{\pi}}\delta_{-byp^{-v_p(y)}\in -b(\chi)+p^i\mathbb{Z}_p} \nonumber\\ &= \delta_{v_p(y) =i-m_{\pi}}\lvert{y}\rvert_p.\nonumber\end{align}
\begin{align} \mathcal{S}_i(y) &= \delta_{v_p(y) =i-m_{\pi}}(1+p^{-1})^{-1}v_0(1)^2\lvert{y}\rvert_p \sum_{b\in (\mathbb{Z}_p/p^{m_{\pi}-i}\mathbb{Z}_p)^{\times}}p^{2i-2m_{\pi}}\delta_{-byp^{-v_p(y)}\in -b(\chi)+p^i\mathbb{Z}_p} \nonumber\\ &= \delta_{v_p(y) =i-m_{\pi}}\lvert{y}\rvert_p.\nonumber\end{align}
Similarly for
![]() $i\geq \lceil {m_{\pi}}/{2}\rceil$
we have
$i\geq \lceil {m_{\pi}}/{2}\rceil$
we have
 \begin{align} \mathcal{S}_i(y) &= \delta_{v_p(y) =i-m_{\pi}}(1+p^{-1})^{-1}v_0(1)^2\lvert{y}\rvert_p \sum_{b\in (\mathbb{Z}_p/p^{m_{\pi}-i}\mathbb{Z}_p)^{\times}}p^{-m_{\pi}}\cdot \delta_{-byp^{-v_p(y)}\in b(\chi)+p^{m_{\pi}-i}\mathbb{Z}_p} \nonumber\\ &= \delta_{v_p(y) =i-m_{\pi}}\lvert{y}\rvert_p.\nonumber\end{align}
\begin{align} \mathcal{S}_i(y) &= \delta_{v_p(y) =i-m_{\pi}}(1+p^{-1})^{-1}v_0(1)^2\lvert{y}\rvert_p \sum_{b\in (\mathbb{Z}_p/p^{m_{\pi}-i}\mathbb{Z}_p)^{\times}}p^{-m_{\pi}}\cdot \delta_{-byp^{-v_p(y)}\in b(\chi)+p^{m_{\pi}-i}\mathbb{Z}_p} \nonumber\\ &= \delta_{v_p(y) =i-m_{\pi}}\lvert{y}\rvert_p.\nonumber\end{align}
Finally consider
![]() $i=m_{\pi}$
. We have
$i=m_{\pi}$
. We have
 \begin{align} \mathcal{S}_{m_{\pi}}(y) &= (1+p^{-1})v_0(1)^2\lvert{y}\rvert_p \lvert{\int_{p^{m_{\pi}}\mathbb{Z}}\chi(x)\lvert{x}\rvert^{2\rho}\psi(x^{-1}y)^{-1}\frac{dx}{\lvert{x}\rvert_p}}\rvert^2 \nonumber \\ &= p^{m_{\pi}}\lvert{y}\rvert_p\cdot \lvert{\int_{p^{m_{\pi}}\mathbb{Z}_p}\chi(x)\lvert{x}\rvert^{2\rho}\psi(x^{-1}y)^{-1}\frac{dx}{\lvert{x}\rvert_p}}\rvert^2.\nonumber\end{align}
\begin{align} \mathcal{S}_{m_{\pi}}(y) &= (1+p^{-1})v_0(1)^2\lvert{y}\rvert_p \lvert{\int_{p^{m_{\pi}}\mathbb{Z}}\chi(x)\lvert{x}\rvert^{2\rho}\psi(x^{-1}y)^{-1}\frac{dx}{\lvert{x}\rvert_p}}\rvert^2 \nonumber \\ &= p^{m_{\pi}}\lvert{y}\rvert_p\cdot \lvert{\int_{p^{m_{\pi}}\mathbb{Z}_p}\chi(x)\lvert{x}\rvert^{2\rho}\psi(x^{-1}y)^{-1}\frac{dx}{\lvert{x}\rvert_p}}\rvert^2.\nonumber\end{align}
Therefore it suffices to compute the remaining integral. By some basic Gauß sum evaluations one gets
Inserting this above concludes the proof since it implies
![]() $\mathcal{S}_{m_{\pi}}(y) =\delta_{v_p(y)>0}\lvert{y}\rvert_p$
.
$\mathcal{S}_{m_{\pi}}(y) =\delta_{v_p(y)>0}\lvert{y}\rvert_p$
.
3·2·3. Supercuspidal representations
Let
![]() $\mathfrak{X}_k$
be the set of character
$\mathfrak{X}_k$
be the set of character
![]() $\chi\colon \mathbb{Q}_p^{\times} \to\mathbb{C}^{\times}$
with
$\chi\colon \mathbb{Q}_p^{\times} \to\mathbb{C}^{\times}$
with
![]() $a(\chi)\leq k$
and
$a(\chi)\leq k$
and
![]() $\chi(p)=1$
. Note that
$\chi(p)=1$
. Note that
For
![]() $\chi\in \mathfrak{X}_k$
and
$\chi\in \mathfrak{X}_k$
and
![]() $m\in \mathbb{Z}$
we will consider the functions
$m\in \mathbb{Z}$
we will consider the functions
![]() $\xi_{\chi}^{(m)} \in \mathcal{C}_c^{\infty}(\mathbb{Q}_p^{\times})$
given by
$\xi_{\chi}^{(m)} \in \mathcal{C}_c^{\infty}(\mathbb{Q}_p^{\times})$
given by
Given any representation
![]() $\pi_p$
we write
$\pi_p$
we write
![]() $\mathcal{K}_{\psi_p}(\pi_p)$
for the corresponding
$\mathcal{K}_{\psi_p}(\pi_p)$
for the corresponding
![]() $\psi_p$
-Kirillov model. Note that this model contains the Schwartz functions so that we have
$\psi_p$
-Kirillov model. Note that this model contains the Schwartz functions so that we have
![]() $\xi_{\chi}^{(m)}\in \mathcal{K}_{\psi_p}(\pi_p)$
. Note that by construction of the Kirillov model we have
$\xi_{\chi}^{(m)}\in \mathcal{K}_{\psi_p}(\pi_p)$
. Note that by construction of the Kirillov model we have
Thus we compute
 \begin{multline} \langle W_{\xi_{\chi_1}^{(m_1)}},W_{\xi_{\chi_2}^{(m_2)}}\rangle = \int_{\mathbb{Q}_p^{\times}}\xi_{\chi_1}^{(m_1)}(y)\overline{\xi_{\chi_2}^{(m_2)}(y)}d^{\times}y = \delta_{m_1=m_2} \int_{p^{-m_1}\mathbb{Z}_p^{\times}}\chi_1(y)\chi_2^{-1}(y)d^{\times}y\\ = \delta_{\substack{m_1=m_2,\\ \chi_1=\chi_2}}.\nonumber\end{multline}
\begin{multline} \langle W_{\xi_{\chi_1}^{(m_1)}},W_{\xi_{\chi_2}^{(m_2)}}\rangle = \int_{\mathbb{Q}_p^{\times}}\xi_{\chi_1}^{(m_1)}(y)\overline{\xi_{\chi_2}^{(m_2)}(y)}d^{\times}y = \delta_{m_1=m_2} \int_{p^{-m_1}\mathbb{Z}_p^{\times}}\chi_1(y)\chi_2^{-1}(y)d^{\times}y\\ = \delta_{\substack{m_1=m_2,\\ \chi_1=\chi_2}}.\nonumber\end{multline}
This suffices to compute
![]() $S_{\pi_p}(a(y))$
for supercuspdial representations
$S_{\pi_p}(a(y))$
for supercuspdial representations
![]() $\pi_p$
.
$\pi_p$
.
Lemma 3·7. Suppose
![]() $\pi_p$
is a twist minimal supercuspidal representation with (exponent)-conductor
$\pi_p$
is a twist minimal supercuspidal representation with (exponent)-conductor
![]() $n_{\pi}$
. Then the following is true:
$n_{\pi}$
. Then the following is true:
-
(i) If
 $n_{\pi}=2m_{\pi}$
, then
$n_{\pi}=2m_{\pi}$
, then  \begin{equation} S_{\pi_p}(a(y)) = \frac{p^{m_{\pi}}}{\zeta_p(1)}\cdot \delta_{y\in p^{-m_{\pi}}\mathbb{Z}_p^{\times}};\nonumber \end{equation}
\begin{equation} S_{\pi_p}(a(y)) = \frac{p^{m_{\pi}}}{\zeta_p(1)}\cdot \delta_{y\in p^{-m_{\pi}}\mathbb{Z}_p^{\times}};\nonumber \end{equation}
-
(ii) If
 $n_{\pi} = 2m_{\pi}-1$
, then
$n_{\pi} = 2m_{\pi}-1$
, then  \begin{equation} S_{\pi_p}(a(y)) = \frac{p^{m_{\pi}}}{\zeta_p(1)}\cdot \delta_{y\in p^{-m_{\pi}}\mathbb{Z}_p^{\times}}+\frac{p^{m_{\pi}-1}}{\zeta_p(1)}\cdot \delta_{y\in p^{1-m_{\pi}}\mathbb{Z}_p^{\times}};\nonumber \end{equation}
\begin{equation} S_{\pi_p}(a(y)) = \frac{p^{m_{\pi}}}{\zeta_p(1)}\cdot \delta_{y\in p^{-m_{\pi}}\mathbb{Z}_p^{\times}}+\frac{p^{m_{\pi}-1}}{\zeta_p(1)}\cdot \delta_{y\in p^{1-m_{\pi}}\mathbb{Z}_p^{\times}};\nonumber \end{equation}
In general we have the bound
Proof. We start with the case
![]() $n_{\pi} = 2m_{\pi}$
. By [
Reference Miyauchi and Yamauchi20
, lemma 4·4] we find that a basis for
$n_{\pi} = 2m_{\pi}$
. By [
Reference Miyauchi and Yamauchi20
, lemma 4·4] we find that a basis for
![]() $\pi^{K_p(m_{\pi})}$
in the Kirillov model is given by
$\pi^{K_p(m_{\pi})}$
in the Kirillov model is given by
Note that we already took advantage of twist-minimality using that
![]() $n_{\chi\pi} =n_{\pi}$
for all
$n_{\chi\pi} =n_{\pi}$
for all
![]() $\chi\in \mathfrak{X}_{m_{\pi}}$
. Our computations above show that this basis is orthonormal (with respect to the Whittaker inner product). Thus we have
$\chi\in \mathfrak{X}_{m_{\pi}}$
. Our computations above show that this basis is orthonormal (with respect to the Whittaker inner product). Thus we have
We turn towards the second case where
![]() $n_{\pi}$
is odd. Then we get the orthonormal basis
$n_{\pi}$
is odd. Then we get the orthonormal basis
It is again easy to compute the desired quantity:
The result follows directly.
3·3. Conclusion
We can now give a decent bound for
![]() $\Phi(z)$
using the Whittaker expansion. We will use the bound (5) and follow the standard procedure.
$\Phi(z)$
using the Whittaker expansion. We will use the bound (5) and follow the standard procedure.
Lemma 3·8. We have
 \begin{equation} \Phi(z) \ll \left(\frac{dT}{y}\right)^{\epsilon}\left( d^{\frac{1}{2}}T^{\frac{1}{6}}+\frac{dT^{\frac{1}{2}}}{y^{\frac{1}{2}}}\right).\nonumber\end{equation}
\begin{equation} \Phi(z) \ll \left(\frac{dT}{y}\right)^{\epsilon}\left( d^{\frac{1}{2}}T^{\frac{1}{6}}+\frac{dT^{\frac{1}{2}}}{y^{\frac{1}{2}}}\right).\nonumber\end{equation}
Proof. Inserting (5) into Lemma 3·1 yields
 \begin{equation} \Phi(g)\ll d^{\frac{1}{2}+\epsilon}T^{\epsilon}\sum_{0 \neq n\in\mathbb{Z}}\frac{\lvert{\lambda_{\pi}\left(n/(n,p^{\infty})\right)}\rvert}{\sqrt{\lvert{n}\rvert}} \lvert{W_{\infty}\left(n\frac{y}{p^{m_{\pi}}}\right)}\rvert.\nonumber\end{equation}
\begin{equation} \Phi(g)\ll d^{\frac{1}{2}+\epsilon}T^{\epsilon}\sum_{0 \neq n\in\mathbb{Z}}\frac{\lvert{\lambda_{\pi}\left(n/(n,p^{\infty})\right)}\rvert}{\sqrt{\lvert{n}\rvert}} \lvert{W_{\infty}\left(n\frac{y}{p^{m_{\pi}}}\right)}\rvert.\nonumber\end{equation}
Estimating the remaining n-sum as for example in [ Reference Templier23 ] or [ Reference Saha21 ] yields the desired result.
4. A bound via the pre-trace formula
The next bound will be derived from the pre-trace inequality. We start by discussing the local test functions. At the archimedean place we closely follow [
Reference Saha21
, section 3.5] and fix
![]() $f_{\infty}$
so that it satisfies:
$f_{\infty}$
so that it satisfies:
-
(1)
 $f_{\infty}(g) = 0$
unless
$f_{\infty}(g) = 0$
unless
 $g\in G(\mathbb{R})^+$
and
$g\in G(\mathbb{R})^+$
and
 $u(g)\leq 1$
;
$u(g)\leq 1$
; -
(2)
 $\hat{f}_{\infty}(\sigma)>0$
for all irreducible spherical unitary principal series representations
$\hat{f}_{\infty}(\sigma)>0$
for all irreducible spherical unitary principal series representations
 $\sigma$
of
$\sigma$
of
 $G(\mathbb{R})$
;
$G(\mathbb{R})$
; -
(3)
 $\hat{f}(\pi_{\infty})\gg 1$
;
$\hat{f}(\pi_{\infty})\gg 1$
; -
(4)
 $\lvert{f_{\infty}(g)}\rvert\leq T$
and if
$\lvert{f_{\infty}(g)}\rvert\leq T$
and if
 $u(g)\geq T^{-2}$
, then
$u(g)\geq T^{-2}$
, then
 $\lvert{f_{\infty}(g)}\rvert\leq T^{\frac{1}{2}}u(g)^{-\frac{1}{4}}$
.
$\lvert{f_{\infty}(g)}\rvert\leq T^{\frac{1}{2}}u(g)^{-\frac{1}{4}}$
.
(The final property is not really necessary because we are ignoring the spectral aspect for now.) Note that
![]() $\hat{f}$
is the spherical transform (also Selberg/Harish–Chandra transform) of f and u(g) is the point-pair invariant on group level.
$\hat{f}$
is the spherical transform (also Selberg/Harish–Chandra transform) of f and u(g) is the point-pair invariant on group level.
At the place
![]() $v=p$
we define multiple test functions:
$v=p$
we define multiple test functions:
 \begin{equation} f_p^{(i)}(g) = \mathbb{1}_{ZK_p}(g) \frac{\overline{\langle \pi(g)\phi_p^{(i)},\phi_p^{(i)}\rangle_{\pi_p}}}{\langle \phi_p^{(i)},\phi_p^{(i)}\rangle_{\pi_p}}.\nonumber\end{equation}
\begin{equation} f_p^{(i)}(g) = \mathbb{1}_{ZK_p}(g) \frac{\overline{\langle \pi(g)\phi_p^{(i)},\phi_p^{(i)}\rangle_{\pi_p}}}{\langle \phi_p^{(i)},\phi_p^{(i)}\rangle_{\pi_p}}.\nonumber\end{equation}
Lemma 4·1. For every irreducible admissible unitary representation
![]() $\sigma$
of
$\sigma$
of
![]() $G(\mathbb{Q}_p)$
the operator
$G(\mathbb{Q}_p)$
the operator
![]() $\sigma(f_p^{(i)})$
is non-negative and self-adjoint. Further we have
$\sigma(f_p^{(i)})$
is non-negative and self-adjoint. Further we have
![]() $\pi_p(f_p^{(i)})\phi_p^{(i)} = \dim_{\mathbb{C}}(\pi_p^{K_p(m_{\pi})})^{-1}\cdot \phi_p^{(i)}$
.
$\pi_p(f_p^{(i)})\phi_p^{(i)} = \dim_{\mathbb{C}}(\pi_p^{K_p(m_{\pi})})^{-1}\cdot \phi_p^{(i)}$
.
Proof. The proof is standard and relies on Schur’s orthogonality relations for irreducible representations of
![]() $K_p$
. To apply this it will be important to keep in mind that
$K_p$
. To apply this it will be important to keep in mind that
![]() $\pi^{K_{p}(m_{\pi})}$
is irreducible.
$\pi^{K_{p}(m_{\pi})}$
is irreducible.
The operators are self-adjoint since
![]() $f_p^{(i)}(g^{-1})=\overline{f_p^{(i)}(g)}$
. To see non-negativity we will show the convolution identity
$f_p^{(i)}(g^{-1})=\overline{f_p^{(i)}(g)}$
. To see non-negativity we will show the convolution identity
Indeed we compute
 \begin{align} [f_p^{(i)}\star f_p^{(i)}](h) &=\int_{Z\backslash G} f_p^{(i)}(g^{-1})f_p^{(i)}(gh)dg \nonumber \\ &= \frac{\mathbb{1}_{ZK}(h)}{{\langle \phi_p^{(i)},\phi_p^{(i)}\rangle_{\pi_p}}^2} \int_{K_p}\langle \pi_p(g)\phi_p^{(i)},\phi_p^{(i)}\rangle_{\pi_p}\overline{\langle \pi_p(gh)\phi_p^{(i)},\phi_p^{(i)}\rangle_{\pi_p}}dk\nonumber \\ &= \dim_{\mathbb{C}}(\pi^{K_{p}(m_{\pi})})^{-1}\frac{\mathbb{1}_{ZK}(h)}{\langle \phi_p^{(i)},\phi_p^{(i)}\rangle_{\pi_p}}\overline{\langle \pi_p(h)\phi_p^{(i)},\phi_p^{(i)}\rangle_{\pi_p}}\nonumber\end{align}
\begin{align} [f_p^{(i)}\star f_p^{(i)}](h) &=\int_{Z\backslash G} f_p^{(i)}(g^{-1})f_p^{(i)}(gh)dg \nonumber \\ &= \frac{\mathbb{1}_{ZK}(h)}{{\langle \phi_p^{(i)},\phi_p^{(i)}\rangle_{\pi_p}}^2} \int_{K_p}\langle \pi_p(g)\phi_p^{(i)},\phi_p^{(i)}\rangle_{\pi_p}\overline{\langle \pi_p(gh)\phi_p^{(i)},\phi_p^{(i)}\rangle_{\pi_p}}dk\nonumber \\ &= \dim_{\mathbb{C}}(\pi^{K_{p}(m_{\pi})})^{-1}\frac{\mathbb{1}_{ZK}(h)}{\langle \phi_p^{(i)},\phi_p^{(i)}\rangle_{\pi_p}}\overline{\langle \pi_p(h)\phi_p^{(i)},\phi_p^{(i)}\rangle_{\pi_p}}\nonumber\end{align}
and the claimed identity follows directly.
It remains to show the final claim. First observe that the image of
![]() $\pi_p(f_p^{(i)})\phi_p^{(i)}$
is obviously
$\pi_p(f_p^{(i)})\phi_p^{(i)}$
is obviously
![]() $K_p(m_{\pi})$
-invariant. Thus it suffices to show that
$K_p(m_{\pi})$
-invariant. Thus it suffices to show that
for any
![]() $w\in \pi_p^{K_p(m_{\pi})}$
But this follows again from the orthogonality relations since
$w\in \pi_p^{K_p(m_{\pi})}$
But this follows again from the orthogonality relations since
![]() $\pi_p^{K_p(m_{\pi})}$
is irreducible (as
$\pi_p^{K_p(m_{\pi})}$
is irreducible (as
![]() $K_p$
-module) and
$K_p$
-module) and
Finally we define the unramified part of the test function
![]() $f_{ur}$
by setting
$f_{ur}$
by setting
 \begin{multline} f_{ur} = \left( \sum_{l\in S} c_l \kappa_l\right)\star \left( \sum_{l\in S} c_l \kappa_l \right)^*+\left( \sum_{l\in S} c_{l^2} \kappa_{l^2}\right)\star \left( \sum_{l\in S} c_{l^2} \kappa_{l^2} \right)^*, \\ \text{ for } c_r=\begin{cases} \frac{\lvert{\lambda_{\pi}(r)}\rvert}{\lambda_{\pi}(r)} &\text{ if $r=l$ or $r=l^2$ for $l\in S$},\\ 0&\text{ else},\end{cases} \nonumber\end{multline}
\begin{multline} f_{ur} = \left( \sum_{l\in S} c_l \kappa_l\right)\star \left( \sum_{l\in S} c_l \kappa_l \right)^*+\left( \sum_{l\in S} c_{l^2} \kappa_{l^2}\right)\star \left( \sum_{l\in S} c_{l^2} \kappa_{l^2} \right)^*, \\ \text{ for } c_r=\begin{cases} \frac{\lvert{\lambda_{\pi}(r)}\rvert}{\lambda_{\pi}(r)} &\text{ if $r=l$ or $r=l^2$ for $l\in S$},\\ 0&\text{ else},\end{cases} \nonumber\end{multline}
for a set of primes S (to be determined) and normalised rth Hecke-operators
![]() $\kappa_r$
. This implements the usual amplification procedure. Finally we define the global test functions
$\kappa_r$
. This implements the usual amplification procedure. Finally we define the global test functions
We introduce
Further let
![]() $\sigma$
denote the irreducible representation of
$\sigma$
denote the irreducible representation of
![]() $\operatorname{GL}_2(\mathbb{Z}/p^{m_{\pi}}\mathbb{Z})$
through which the irreducible
$\operatorname{GL}_2(\mathbb{Z}/p^{m_{\pi}}\mathbb{Z})$
through which the irreducible
![]() $K_p$
-module
$K_p$
-module
![]() $\pi^{K_p(m_{\pi})}$
factors. This is a representation of a finite group and we write
$\pi^{K_p(m_{\pi})}$
factors. This is a representation of a finite group and we write
![]() $\chi_{\sigma}$
for its character. Finally we define the coefficients
$\chi_{\sigma}$
for its character. Finally we define the coefficients
![]() $y_r$
by linearising the convolutions of Hecke-operators in the definition of
$y_r$
by linearising the convolutions of Hecke-operators in the definition of
![]() $f_{ur}$
. More precisely we write
$f_{ur}$
. More precisely we write
This can be compared to the analogous expression in [ Reference Saha21 , section 7].
The following pre-trace inequality provides the transition to the counting problem.
Lemma 4·2. For
![]() $z\in \mathcal{F}$
we have
$z\in \mathcal{F}$
we have
 \begin{equation} \frac{(\sharp S)^2}{\dim_{\mathbb{C}}\pi_p^{K_p(m_{\pi})}} \cdot \Phi(z)^2 \ll \sum_{r} \frac{\lvert{y_r}\rvert}{\sqrt{r}} \sum_{g\in \operatorname{GL}_2(\mathbb{Z}/p^{m_{\pi}}\mathbb{Z})} \lvert{\chi_{\sigma}(g)}\rvert \sum_{A\in M(l,g)} \lvert{f_{\infty}(u(Az,z))}\rvert.\nonumber\end{equation}
\begin{equation} \frac{(\sharp S)^2}{\dim_{\mathbb{C}}\pi_p^{K_p(m_{\pi})}} \cdot \Phi(z)^2 \ll \sum_{r} \frac{\lvert{y_r}\rvert}{\sqrt{r}} \sum_{g\in \operatorname{GL}_2(\mathbb{Z}/p^{m_{\pi}}\mathbb{Z})} \lvert{\chi_{\sigma}(g)}\rvert \sum_{A\in M(l,g)} \lvert{f_{\infty}(u(Az,z))}\rvert.\nonumber\end{equation}
Proof. We start by considering the spectral expansion of the automorphic kernel
![]() $k_{f^{(i)}}$
associated to the self-adjoint operators
$k_{f^{(i)}}$
associated to the self-adjoint operators
![]() $R(f^{(i)})$
and dropping all terms except
$R(f^{(i)})$
and dropping all terms except
![]() $\phi_i$
. The latter is possible by positivity. We obtain
$\phi_i$
. The latter is possible by positivity. We obtain
 \begin{equation} \frac{(\sharp S)^2}{\dim_{\mathbb{C}}\pi_p^{K_p(m_{\pi})}} \cdot \phi_i(g_{\infty})^2 \leq k_{f^{(i)}}(g,g) = \sum_{r}y_r \sum_{\gamma\in Z(\mathbb{Q})\backslash G(\mathbb{Q})} f_p^{(i)}(\gamma)\kappa_r(\gamma)f_{\infty}(g_{\infty}^{-1}\gamma g_{\infty}).\nonumber\end{equation}
\begin{equation} \frac{(\sharp S)^2}{\dim_{\mathbb{C}}\pi_p^{K_p(m_{\pi})}} \cdot \phi_i(g_{\infty})^2 \leq k_{f^{(i)}}(g,g) = \sum_{r}y_r \sum_{\gamma\in Z(\mathbb{Q})\backslash G(\mathbb{Q})} f_p^{(i)}(\gamma)\kappa_r(\gamma)f_{\infty}(g_{\infty}^{-1}\gamma g_{\infty}).\nonumber\end{equation}
We now sum this inequality over i to obtain
 \begin{equation} \frac{(\sharp S)^2}{\dim_{\mathbb{C}}\pi_p^{K_p(m_{\pi})}}\Phi(g_{\infty})^2 \leq \sum_r y_r \sum_{\gamma\in Z(\mathbb{Q})\backslash G(\mathbb{Q})} \left(\sum_{i=1}^d f_p^{(i)}(\gamma)\right) \kappa_r(\gamma)f_{\infty}(g_{\infty}^{-1}\gamma g_{\infty}).\nonumber\end{equation}
\begin{equation} \frac{(\sharp S)^2}{\dim_{\mathbb{C}}\pi_p^{K_p(m_{\pi})}}\Phi(g_{\infty})^2 \leq \sum_r y_r \sum_{\gamma\in Z(\mathbb{Q})\backslash G(\mathbb{Q})} \left(\sum_{i=1}^d f_p^{(i)}(\gamma)\right) \kappa_r(\gamma)f_{\infty}(g_{\infty}^{-1}\gamma g_{\infty}).\nonumber\end{equation}
Recall that the test functions
![]() $f_p^{(i)}$
are supported in
$f_p^{(i)}$
are supported in
![]() $ZK_p$
. Thus, after choosing a suitable representative for
$ZK_p$
. Thus, after choosing a suitable representative for
![]() $\gamma$
modulo
$\gamma$
modulo
![]() $Z(\mathbb{Q})$
, we can assume that
$Z(\mathbb{Q})$
, we can assume that
![]() $\gamma\in K_p$
and write
$\gamma\in K_p$
and write
![]() $\overline{\gamma}$
for the image of
$\overline{\gamma}$
for the image of
![]() $\gamma$
in
$\gamma$
in
![]() $\operatorname{GL}_2(\mathbb{Z}/p^{m_{\pi}}\mathbb{Z})$
. For such
$\operatorname{GL}_2(\mathbb{Z}/p^{m_{\pi}}\mathbb{Z})$
. For such
![]() $\gamma$
we get
$\gamma$
we get
 \begin{equation} \sum_{i=1}^d f_p^{(i)}(\gamma) = \chi_{\sigma}(\overline{\gamma}).\nonumber\end{equation}
\begin{equation} \sum_{i=1}^d f_p^{(i)}(\gamma) = \chi_{\sigma}(\overline{\gamma}).\nonumber\end{equation}
The rest of the argument is standard and can for example be found in [ Reference Saha21 ].
By the choice of
![]() $f_{\infty}$
we can already eliminate the archimedean influence from the right-hand side. (Note that we are not aiming to amplify in the T-aspect.)
$f_{\infty}$
we can already eliminate the archimedean influence from the right-hand side. (Note that we are not aiming to amplify in the T-aspect.)
Corollary 4·3. For
![]() $z\in \mathcal{F}$
we have
$z\in \mathcal{F}$
we have
 \begin{equation} \frac{(\sharp S)^2}{\dim_{\mathbb{C}}\pi_p^{K_p(m_{\pi})}} \cdot \Phi(z)^2 \ll T \sum_{g\in \operatorname{GL}_2(\mathbb{Z}/p^{m_{\pi}}\mathbb{Z})} \lvert{\chi_{\sigma}(g)}\rvert \sum_{r} \frac{\lvert{y_r}\rvert}{\sqrt{r}} \cdot \sharp M_z(r,g),\nonumber\end{equation}
\begin{equation} \frac{(\sharp S)^2}{\dim_{\mathbb{C}}\pi_p^{K_p(m_{\pi})}} \cdot \Phi(z)^2 \ll T \sum_{g\in \operatorname{GL}_2(\mathbb{Z}/p^{m_{\pi}}\mathbb{Z})} \lvert{\chi_{\sigma}(g)}\rvert \sum_{r} \frac{\lvert{y_r}\rvert}{\sqrt{r}} \cdot \sharp M_z(r,g),\nonumber\end{equation}
for
This last corollary tells us that we need to control the character
![]() $\chi_{\sigma}$
and solve a counting problem estimating
$\chi_{\sigma}$
and solve a counting problem estimating
![]() $M_z(r,g)$
.
$M_z(r,g)$
.
To estimate the character we need to define certain level sets.
Note that
![]() $K_{m,m} = \{1\}$
and
$K_{m,m} = \{1\}$
and
![]() $K_{m,0} = G(\mathbb{Z}/p^m\mathbb{Z})$
.
$K_{m,0} = G(\mathbb{Z}/p^m\mathbb{Z})$
.
Before we continue let us make a remark concerning notation. We will write
![]() $A\neg B = A\cap B^c$
for the set-theoretic difference. We are not using
$A\neg B = A\cap B^c$
for the set-theoretic difference. We are not using
![]() $A\setminus B$
, since it may be confused with the quotient when A and B are groups.
$A\setminus B$
, since it may be confused with the quotient when A and B are groups.
Lemma 4·4. Suppose
![]() $p>3$
. Let
$p>3$
. Let
![]() $\pi$
belong to Case 1, 2 or 3·1. Then, for
$\pi$
belong to Case 1, 2 or 3·1. Then, for
![]() $0\leq \lambda < m_{\pi}$
and
$0\leq \lambda < m_{\pi}$
and
![]() $g\in Z\cdot K_{m_{\pi},\lambda}\neg Z\cdot K_{m_{\pi},\lambda+1}$
we have
$g\in Z\cdot K_{m_{\pi},\lambda}\neg Z\cdot K_{m_{\pi},\lambda+1}$
we have
If
![]() $\pi$
belongs to Case 3·2 and
$\pi$
belongs to Case 3·2 and
![]() $\lambda$
and g are as above, then we have the slightly weaker bound
$\lambda$
and g are as above, then we have the slightly weaker bound
Furthermore, let
![]() $h\in G(\mathbb{Z}/p^m\mathbb{Z})$
be a diagonal matrix such that
$h\in G(\mathbb{Z}/p^m\mathbb{Z})$
be a diagonal matrix such that
![]() $G(\mathbb{Z}/p^m\mathbb{Z})=Z\cdot \operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})\sqcup hZ\cdot \operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})$
. Then the same estimates hold for
$G(\mathbb{Z}/p^m\mathbb{Z})=Z\cdot \operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})\sqcup hZ\cdot \operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})$
. Then the same estimates hold for
![]() $hZ \cdot K_{m_{\pi},\lambda}\neg hZ\cdot K_{m_{\pi},\lambda+1}$
, where
$hZ \cdot K_{m_{\pi},\lambda}\neg hZ\cdot K_{m_{\pi},\lambda+1}$
, where
![]() $\det(h)$
is not a square modulo
$\det(h)$
is not a square modulo
![]() $p^{m_{\pi}}$
.
$p^{m_{\pi}}$
.
The representations of
![]() $\operatorname{GL}_2$
over finite rings such as
$\operatorname{GL}_2$
over finite rings such as
![]() $\mathbb{Z}/p^m\mathbb{Z}$
and their characters are well studied but explicit estimates for the characters as needed here seem to be hard to find. We choose to use the character tables for
$\mathbb{Z}/p^m\mathbb{Z}$
and their characters are well studied but explicit estimates for the characters as needed here seem to be hard to find. We choose to use the character tables for
![]() $\operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})$
computed by Kutzko [
Reference Kutzko15
]. This makes it necessary to pass from
$\operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})$
computed by Kutzko [
Reference Kutzko15
]. This makes it necessary to pass from
![]() $\operatorname{SL}_2$
to
$\operatorname{SL}_2$
to
![]() $\operatorname{GL}_2$
using Mackey Theory. Note that the character values in question were calculated in [
Reference Leigh, Cliff and Wen3
]. However, they remain hard to extract and we hope our approach is more transparent.
$\operatorname{GL}_2$
using Mackey Theory. Note that the character values in question were calculated in [
Reference Leigh, Cliff and Wen3
]. However, they remain hard to extract and we hope our approach is more transparent.
Proof. As mentioned above our starting point are well-known character tables for
![]() $\operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})$
. These are upgraded to
$\operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})$
. These are upgraded to
![]() $\operatorname{GL}_2(\mathbb{Z}/p^m\mathbb{Z})$
via a simple application of Mackey theory.
$\operatorname{GL}_2(\mathbb{Z}/p^m\mathbb{Z})$
via a simple application of Mackey theory.
Recall that p is assumed to be odd, write
![]() $\omega_{\sigma}$
for the central character of
$\omega_{\sigma}$
for the central character of
![]() $\sigma$
and let
$\sigma$
and let
![]() $\tilde{\sigma}$
be an irreducible component of
$\tilde{\sigma}$
be an irreducible component of
![]() $\sigma\vert_{\operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})}$
. Further, fix h such that
$\sigma\vert_{\operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})}$
. Further, fix h such that
![]() $\operatorname{GL}_2(\mathbb{Z}/p^m\mathbb{Z}) = Z\operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})\cup h\cdot Z\operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})$
and write
$\operatorname{GL}_2(\mathbb{Z}/p^m\mathbb{Z}) = Z\operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})\cup h\cdot Z\operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})$
and write
![]() $\tilde{\sigma}^h(g) = \tilde{\sigma}(hgh^{-1})$
. If
$\tilde{\sigma}^h(g) = \tilde{\sigma}(hgh^{-1})$
. If
![]() $\tilde{\sigma}\not\cong\tilde{\sigma}^h$
, then
$\tilde{\sigma}\not\cong\tilde{\sigma}^h$
, then
In this case
![]() $\sigma\vert_{\operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})}=\tilde{\sigma}+\tilde{\sigma}^h$
and we have
$\sigma\vert_{\operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})}=\tilde{\sigma}+\tilde{\sigma}^h$
and we have
![]() $\chi_{\sigma}(zs)=w_{\sigma}(z)[\chi_{\tilde{\sigma}}(s)+\chi_{\tilde{\sigma}}^h(s)]$
for
$\chi_{\sigma}(zs)=w_{\sigma}(z)[\chi_{\tilde{\sigma}}(s)+\chi_{\tilde{\sigma}}^h(s)]$
for
![]() $z\in Z$
and
$z\in Z$
and
![]() $s\in \operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})$
. Otherwise, if
$s\in \operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})$
. Otherwise, if
![]() $\tilde{\sigma}\cong\tilde{\sigma}^h$
, then
$\tilde{\sigma}\cong\tilde{\sigma}^h$
, then
where
![]() $\sigma'$
is another irreducible representation of
$\sigma'$
is another irreducible representation of
![]() $\operatorname{GL}_2(\mathbb{Z}/p^m_{\pi}\mathbb{Z})$
. Here we have
$\operatorname{GL}_2(\mathbb{Z}/p^m_{\pi}\mathbb{Z})$
. Here we have
![]() $\sigma\vert_{\operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})}=\tilde{\sigma}$
and obtain
$\sigma\vert_{\operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})}=\tilde{\sigma}$
and obtain
![]() $\chi_{\sigma}(zs) = \omega_{\sigma}(z)\chi_{\tilde{\sigma}}(s)$
.
$\chi_{\sigma}(zs) = \omega_{\sigma}(z)\chi_{\tilde{\sigma}}(s)$
.
The subgroups
![]() $K_{m,\lambda}$
are all normal in
$K_{m,\lambda}$
are all normal in
![]() $K_{m,0}$
, so that the sets
$K_{m,0}$
, so that the sets
![]() $Z\cdot K_{m_{\pi},\lambda}\neg K_{m_{\pi},\lambda+1}$
and
$Z\cdot K_{m_{\pi},\lambda}\neg K_{m_{\pi},\lambda+1}$
and
![]() $hZ \cdot K_{m_{\pi},\lambda}\neg hZ\cdot K_{m_{\pi},\lambda+1}$
can be decomposed into (disjoint)
$hZ \cdot K_{m_{\pi},\lambda}\neg hZ\cdot K_{m_{\pi},\lambda+1}$
can be decomposed into (disjoint)
![]() $\operatorname{GL}_2(\mathbb{Z}/p^{m_{\pi}})$
conjugacy classes. We focus on estimating
$\operatorname{GL}_2(\mathbb{Z}/p^{m_{\pi}})$
conjugacy classes. We focus on estimating
![]() $\chi_{\sigma}$
for
$\chi_{\sigma}$
for
The case
![]() $g\in hZ\cdot \operatorname{SL}_2(\mathbb{Z}/p^mZ)$
is similar.
$g\in hZ\cdot \operatorname{SL}_2(\mathbb{Z}/p^mZ)$
is similar.
Let us recall that non-trivial irreducible representations of
![]() $\operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})$
with
$\operatorname{SL}_2(\mathbb{Z}/p^m\mathbb{Z})$
with
![]() $m>1$
have dimensions
$m>1$
have dimensions
![]() $p^m(1-p^{-1})$
,
$p^m(1-p^{-1})$
,
![]() $p^m(1+p^{-1})$
or
$p^m(1+p^{-1})$
or
![]() ${1}/{2}p^m(1-p^{-2})$
. If
${1}/{2}p^m(1-p^{-2})$
. If
![]() $m=1$
, we are dealing with the representation theory of
$m=1$
, we are dealing with the representation theory of
![]() $\operatorname{SL}_2(\mathbb{F}_p)$
which was for example studied by Schur in [
Reference Schur22
]. It turns out that, besides the normal representations of dimensions
$\operatorname{SL}_2(\mathbb{F}_p)$
which was for example studied by Schur in [
Reference Schur22
]. It turns out that, besides the normal representations of dimensions
![]() $p+1$
and
$p+1$
and
![]() $p-1$
, we have certain special cases. Indeed, we have the Steinberg representation
$p-1$
, we have certain special cases. Indeed, we have the Steinberg representation
![]() $\rho_{\mathrm{St}}$
of dimension p and two irreducible representations
$\rho_{\mathrm{St}}$
of dimension p and two irreducible representations
![]() $\rho_+$
and
$\rho_+$
and
![]() $\rho_+^h$
(resp.
$\rho_+^h$
(resp.
![]() $\rho_-$
and
$\rho_-$
and
![]() $\rho_-^h$
) of dimension
$\rho_-^h$
) of dimension
![]() ${1}/{2}(p+1)$
(resp.
${1}/{2}(p+1)$
(resp.
![]() ${1}/{2}(p-1)$
).
${1}/{2}(p-1)$
).
We now treat each case appearing in Lemma 2·1 separately.
-
(a) Suppose
 $\pi$
belongs to Case 1. We recall from Lemma 2·2 that in this case
$\pi$
belongs to Case 1. We recall from Lemma 2·2 that in this case
 $\sigma$
has dimension
$\sigma$
has dimension
 $p^{m_{\pi}}(1+{1}/{p})$
. We need to look into two sub cases:
$p^{m_{\pi}}(1+{1}/{p})$
. We need to look into two sub cases:-
(i) Suppose
 $m_{\pi}=1$
. In this case two situations can occur. If
$m_{\pi}=1$
. In this case two situations can occur. If
 $\sigma$
stays irreducible when restricted to
$\sigma$
stays irreducible when restricted to
 $\operatorname{SL}_2(\mathbb{Z}/p\mathbb{Z})$
, then we are in case (8) and
$\operatorname{SL}_2(\mathbb{Z}/p\mathbb{Z})$
, then we are in case (8) and
 $\vert\chi_{\sigma}(zs)\vert =\vert \chi_{\tilde{\sigma}}(s)\vert$
with an irreducible representation
$\vert\chi_{\sigma}(zs)\vert =\vert \chi_{\tilde{\sigma}}(s)\vert$
with an irreducible representation
 $\tilde{\sigma}$
of
$\tilde{\sigma}$
of
 $\operatorname{SL}_2(\mathbb{Z}/p\mathbb{Z})$
of dimension
$\operatorname{SL}_2(\mathbb{Z}/p\mathbb{Z})$
of dimension
 $p+1$
. On the other hand, if
$p+1$
. On the other hand, if
 $\sigma\vert_{\operatorname{SL}_2(\mathbb{Z}/p\mathbb{Z})} = \rho_+\oplus\rho_-$
, then we have
$\sigma\vert_{\operatorname{SL}_2(\mathbb{Z}/p\mathbb{Z})} = \rho_+\oplus\rho_-$
, then we have
 $\vert\chi_{\sigma}(zs)\vert =\vert \chi_{\rho_+}(s)+\chi_{\rho_+^h}(s)\vert$
. In both cases one concludes by looking up the corresponding character values, for example in [
Reference Kutzko15
, table V]. (Alternatively one can compute the character of
$\vert\chi_{\sigma}(zs)\vert =\vert \chi_{\rho_+}(s)+\chi_{\rho_+^h}(s)\vert$
. In both cases one concludes by looking up the corresponding character values, for example in [
Reference Kutzko15
, table V]. (Alternatively one can compute the character of
 $\sigma$
directly by observing that it can be realised as an irreducible parabolically induced representation of
$\sigma$
directly by observing that it can be realised as an irreducible parabolically induced representation of
 $\operatorname{GL}(\mathbb{F}_p)$
.)
$\operatorname{GL}(\mathbb{F}_p)$
.) -
(ii) Suppose
 $m_{\pi}>1$
. By looking at the possible dimensions of non-trivial irreducible representations of
$m_{\pi}>1$
. By looking at the possible dimensions of non-trivial irreducible representations of
 $\operatorname{SL}_2(\mathbb{Z}/p^{m_{\pi}}\mathbb{Z})$
we see that
$\operatorname{SL}_2(\mathbb{Z}/p^{m_{\pi}}\mathbb{Z})$
we see that
 $\tilde{\sigma}$
must have dimension
$\tilde{\sigma}$
must have dimension
 $p^{m_{\pi}}(1+{1}/{p})$
as well. Thus
$p^{m_{\pi}}(1+{1}/{p})$
as well. Thus
 $\sigma$
remains irreducible when restricted to
$\sigma$
remains irreducible when restricted to
 $\operatorname{SL}_2(\mathbb{Z}/p^{m_{\pi}}\mathbb{Z})$
and we are in the situation of (8). We have
$\operatorname{SL}_2(\mathbb{Z}/p^{m_{\pi}}\mathbb{Z})$
and we are in the situation of (8). We have
 $\vert \chi_{\sigma}(zs)\vert =\vert \chi_{\tilde{\sigma}}(s)\vert$
and the relevant character values for
$\vert \chi_{\sigma}(zs)\vert =\vert \chi_{\tilde{\sigma}}(s)\vert$
and the relevant character values for
 $\chi_{\tilde{\sigma}}$
can be found in [
Reference Kutzko15
, table III].
$\chi_{\tilde{\sigma}}$
can be found in [
Reference Kutzko15
, table III].
-
-
(b) Suppose
 $\pi$
belongs to Case 2. Here we automatically have
$\pi$
belongs to Case 2. Here we automatically have
 $m_{\pi}=1$
and applying Lemma 2·2 yields that the dimension of
$m_{\pi}=1$
and applying Lemma 2·2 yields that the dimension of
 $\sigma$
is p. We conclude that we are in the situation of (8) and
$\sigma$
is p. We conclude that we are in the situation of (8) and
 $\tilde{\sigma}=\rho_{}$
is the Steinberg representation. We have
$\tilde{\sigma}=\rho_{}$
is the Steinberg representation. We have
 $\vert \chi_{\sigma}(zs)\vert = \vert\chi_{\tilde{\sigma}}(s)\vert = 1$
as can be seen from [
Reference Kutzko15
, table V]. (Alternatively one could note that
$\vert \chi_{\sigma}(zs)\vert = \vert\chi_{\tilde{\sigma}}(s)\vert = 1$
as can be seen from [
Reference Kutzko15
, table V]. (Alternatively one could note that
 $\sigma$
itself is the Steinberg representation of
$\sigma$
itself is the Steinberg representation of
 $\operatorname{GL}_2(\mathbb{F}_p)$
, whose character is also well known.)
$\operatorname{GL}_2(\mathbb{F}_p)$
, whose character is also well known.) -
(c) Suppose
 $\pi$
belongs to Case 3·1. An application of Lemma 2·2 yields that
$\pi$
belongs to Case 3·1. An application of Lemma 2·2 yields that
 $\sigma$
has dimension
$\sigma$
has dimension
 $p^{m_{\pi}}(1-{1}/{p})$
. As in Case 1 we need to distinguish two sub cases:
$p^{m_{\pi}}(1-{1}/{p})$
. As in Case 1 we need to distinguish two sub cases:-
(i) Suppose
 $m_{\pi}=1$
. We can have
$m_{\pi}=1$
. We can have
 $\sigma\vert_{\operatorname{SL}_2(\mathbb{Z}/p\mathbb{Z})}=\rho_-\oplus\rho_-^h$
. In this case we estimate
$\sigma\vert_{\operatorname{SL}_2(\mathbb{Z}/p\mathbb{Z})}=\rho_-\oplus\rho_-^h$
. In this case we estimate
 $\vert\chi_{\sigma}(zs)\vert =\vert \chi_{\rho_+}(s)+\chi_{\rho_+^h}(s)\vert$
. Otherwise,
$\vert\chi_{\sigma}(zs)\vert =\vert \chi_{\rho_+}(s)+\chi_{\rho_+^h}(s)\vert$
. Otherwise,
 $\sigma\vert_{\operatorname{SL}_2(\mathbb{Z}/p\mathbb{Z})} = \tilde{\sigma}$
for an irreducible representation
$\sigma\vert_{\operatorname{SL}_2(\mathbb{Z}/p\mathbb{Z})} = \tilde{\sigma}$
for an irreducible representation
 $\tilde{\sigma}$
of
$\tilde{\sigma}$
of
 $\operatorname{SL}_2(\mathbb{Z}/p\mathbb{Z})$
of dimension
$\operatorname{SL}_2(\mathbb{Z}/p\mathbb{Z})$
of dimension
 $p-1$
. Here we simply have
$p-1$
. Here we simply have
 $\vert\chi_{\sigma}(zs)\vert =\vert \chi_{\tilde{\sigma}}(s)\vert$
. The desired estimate is produced by looking up the relevant character values. These can be found in [
Reference Kutzko15
, table V] for example. (Alternatively one can observe that
$\vert\chi_{\sigma}(zs)\vert =\vert \chi_{\tilde{\sigma}}(s)\vert$
. The desired estimate is produced by looking up the relevant character values. These can be found in [
Reference Kutzko15
, table V] for example. (Alternatively one can observe that
 $\sigma$
is a cuspidal representation of
$\sigma$
is a cuspidal representation of
 $\operatorname{GL}_2(\mathbb{F}_p)$
. It turns out that values of characters of cuspidal representations are even known for
$\operatorname{GL}_2(\mathbb{F}_p)$
. It turns out that values of characters of cuspidal representations are even known for
 $\operatorname{GL}_n(\mathbb{F}_p)$
, see for example [
Reference Green10
].)
$\operatorname{GL}_n(\mathbb{F}_p)$
, see for example [
Reference Green10
].) -
(ii) Suppose
 $m_{\pi}>1$
. In this case we again must be in the situation of (8). In particular,
$m_{\pi}>1$
. In this case we again must be in the situation of (8). In particular,
 $\tilde{\sigma}$
is a representation of dimension
$\tilde{\sigma}$
is a representation of dimension
 $p^{m_{\pi}}(1-{1}/{p})$
. The relevant character values can be found in [
Reference Kutzko15
, table III].
$p^{m_{\pi}}(1-{1}/{p})$
. The relevant character values can be found in [
Reference Kutzko15
, table III].
-
-
(d) Suppose
 $\pi$
belongs to Case 3.2. Note that in this case we automatically have
$\pi$
belongs to Case 3.2. Note that in this case we automatically have
 $m_{\pi}>1$
. Furthermore, Lemma 2·2 tells us that the dimension of
$m_{\pi}>1$
. Furthermore, Lemma 2·2 tells us that the dimension of
 $\sigma$
is
$\sigma$
is
 $p^{m_{\pi}}(1-{1}/{p^2})$
. Thus, taking the dimensions of (irreducible) representations of
$p^{m_{\pi}}(1-{1}/{p^2})$
. Thus, taking the dimensions of (irreducible) representations of
 $\operatorname{SL}_2(\mathbb{Z}/p^{m_{\pi}}\mathbb{Z})$
into account, we see that
$\operatorname{SL}_2(\mathbb{Z}/p^{m_{\pi}}\mathbb{Z})$
into account, we see that
 $\sigma\vert_{\operatorname{SL}_2(\mathbb{Z}/p^{m_{\pi}}\mathbb{Z})}$
must be reducible, so that we are in the situation of (7). We estimate
$\sigma\vert_{\operatorname{SL}_2(\mathbb{Z}/p^{m_{\pi}}\mathbb{Z})}$
must be reducible, so that we are in the situation of (7). We estimate
 $\vert\chi_{\sigma}(zs)\vert \leq 2\max(\vert\chi_{\tilde{\sigma}}(s)\vert,\vert\chi_{\tilde{\sigma}^h}(s)\vert)$
. Both representations
$\vert\chi_{\sigma}(zs)\vert \leq 2\max(\vert\chi_{\tilde{\sigma}}(s)\vert,\vert\chi_{\tilde{\sigma}^h}(s)\vert)$
. Both representations
 $\tilde{\sigma}$
and
$\tilde{\sigma}$
and
 $\tilde{\sigma}^h$
must have dimension
$\tilde{\sigma}^h$
must have dimension
 ${1}/{2}p^{m_{\pi}}(1-{1}/{p^2})$
and the corresponding character values can be found in [
Reference Kutzko15
, table IV].Footnote 1
${1}/{2}p^{m_{\pi}}(1-{1}/{p^2})$
and the corresponding character values can be found in [
Reference Kutzko15
, table IV].Footnote 1
This exhausts all the cases and the proof is complete.
Before continuing we will discuss our choice of S. But first recall that
![]() $d=\dim_{\mathbb{C}}\pi_p^{K_p(m_{\pi})} \asymp p^{m_{\pi}}$
. Further note that
$d=\dim_{\mathbb{C}}\pi_p^{K_p(m_{\pi})} \asymp p^{m_{\pi}}$
. Further note that
![]() $y_r=0$
unless
$y_r=0$
unless
![]() $r=1,l_1,l_1l_2,l_1^2l_2^2$
for
$r=1,l_1,l_1l_2,l_1^2l_2^2$
for
![]() $l_1,l_2\in S$
. Put
$l_1,l_2\in S$
. Put
![]() $\Lambda = d^{\frac{1}{3}}$
or
$\Lambda = d^{\frac{1}{3}}$
or
![]() $\Lambda= d^{\frac{1}{6}}$
. This is a slight spoiler but for experts in amplification it should be no surprise that this is the optimal size of the amplifier in this setting. Let
$\Lambda= d^{\frac{1}{6}}$
. This is a slight spoiler but for experts in amplification it should be no surprise that this is the optimal size of the amplifier in this setting. Let
By the prime number theorem (assuming d is sufficiently large, which is no problem) we have
![]() $\sharp S \sim \Lambda/\log(\Lambda)$
, but for us the following crude bound suffices
$\sharp S \sim \Lambda/\log(\Lambda)$
, but for us the following crude bound suffices
Before we are ready to prove our key estimate we need to establish some counting results. Let
The case
![]() $\lambda=0$
is easily handled using existing results. For example taking
$\lambda=0$
is easily handled using existing results. For example taking
![]() $N=\delta=1$
in [
Reference Templier23
, proposition 6·1]. We follow standard procedure and write
$N=\delta=1$
in [
Reference Templier23
, proposition 6·1]. We follow standard procedure and write
Here the subscript
![]() $\star$
indicated that we are dealing with generic matrices
$\star$
indicated that we are dealing with generic matrices
![]() $A=\left(\begin{matrix} a& b\\ c&d\end{matrix}\right)$
with
$A=\left(\begin{matrix} a& b\\ c&d\end{matrix}\right)$
with
![]() $c\neq 0$
and
$c\neq 0$
and
![]() $(a+d)^2\neq 4r$
. On the other hand u stands for unipotent so that
$(a+d)^2\neq 4r$
. On the other hand u stands for unipotent so that
![]() $A\in M_{z,u}^{(\lambda)}(r)$
if and only if
$A\in M_{z,u}^{(\lambda)}(r)$
if and only if
![]() $c=0$
. Finally,
$c=0$
. Finally,
![]() $A\in M_{z,p}^{(\lambda)}(r)$
if
$A\in M_{z,p}^{(\lambda)}(r)$
if
![]() $c\neq 0$
and
$c\neq 0$
and
![]() $(a+d)^2= 4r$
. These are the parabolic matrices.
$(a+d)^2= 4r$
. These are the parabolic matrices.
Counting the contribution of generic matrices is a standard lattice point counting argument. Note that, since we can take z in the classical fundamental domain for
![]() $\operatorname{SL}_2(\mathbb{Z})$
, this argument can be simplified. Indeed, in contrast to [
Reference Harcos and Templier11
, 23] we do not need to invoke Atkin–Lehner operators here.
$\operatorname{SL}_2(\mathbb{Z})$
, this argument can be simplified. Indeed, in contrast to [
Reference Harcos and Templier11
, 23] we do not need to invoke Atkin–Lehner operators here.
Lemma 4·5. For
![]() $\lambda>1$
and
$\lambda>1$
and
![]() $y\geq {\sqrt{3}}/{2}$
we have
$y\geq {\sqrt{3}}/{2}$
we have
 \begin{equation} \sum_{r\asymp K} [\sharp M_{z,\star}^{(\lambda)}(r)+M_{z,p}^{(\lambda)}(r)] \ll \frac{K^{\frac{3}{2}}}{p^\lambda}+\frac{K^2}{p^{2\lambda}}\nonumber\end{equation}
\begin{equation} \sum_{r\asymp K} [\sharp M_{z,\star}^{(\lambda)}(r)+M_{z,p}^{(\lambda)}(r)] \ll \frac{K^{\frac{3}{2}}}{p^\lambda}+\frac{K^2}{p^{2\lambda}}\nonumber\end{equation}
and
 \begin{equation} \sum_{\substack{r\asymp K, \\ r=\square}} \sharp M_{z,\star}^{(\lambda)}(r) \ll \frac{K^{1+\epsilon}}{p^\lambda}+\frac{K^{\frac{3}{2}+\epsilon}}{p^{2\lambda}}.\nonumber\end{equation}
\begin{equation} \sum_{\substack{r\asymp K, \\ r=\square}} \sharp M_{z,\star}^{(\lambda)}(r) \ll \frac{K^{1+\epsilon}}{p^\lambda}+\frac{K^{\frac{3}{2}+\epsilon}}{p^{2\lambda}}.\nonumber\end{equation}
We closely follow the argument in [ Reference Templier23 ].
Proof. Write
![]() $A=\left(\begin{matrix} a&b \\ c & d\end{matrix}\right)$
. Since
$A=\left(\begin{matrix} a&b \\ c & d\end{matrix}\right)$
. Since
![]() $c\neq0$
and
$c\neq0$
and
![]() $c\ll \sqrt{r}y^{-1}$
we have
$c\ll \sqrt{r}y^{-1}$
we have
![]() $\ll {K^{\frac{1}{2}}}/{p^{\lambda}y}$
choices for c. Similarly, using the bound
$\ll {K^{\frac{1}{2}}}/{p^{\lambda}y}$
choices for c. Similarly, using the bound
![]() $\lvert{a+d}\rvert\ll\sqrt{K}$
, we have
$\lvert{a+d}\rvert\ll\sqrt{K}$
, we have
![]() $\ll K^{\frac{1}{2}}$
possibilities to choose
$\ll K^{\frac{1}{2}}$
possibilities to choose
![]() $a+d$
. Finally, we have the bound
$a+d$
. Finally, we have the bound
Write
![]() $b=p^{\lambda}b'$
and consider the lattice
$b=p^{\lambda}b'$
and consider the lattice
![]() $L=\langle z,p^{\lambda}\rangle$
. Note that L has cocolume
$L=\langle z,p^{\lambda}\rangle$
. Note that L has cocolume
![]() $\asymp p^{\lambda}y$
and first successive minima
$\asymp p^{\lambda}y$
and first successive minima
![]() $\gg 1$
(since
$\gg 1$
(since
![]() $y\gg 1$
). Let B be the ball of radius
$y\gg 1$
). Let B be the ball of radius
![]() $2\sqrt{K}y$
around
$2\sqrt{K}y$
around
![]() $-cz^2$
. Then we have
$-cz^2$
. Then we have
We have counted the number of possibilities for the admissible quadruples
![]() $(c,b',a+d,a-d)$
. Since each of those quadruples uniquely determines a matrix A we have established
$(c,b',a+d,a-d)$
. Since each of those quadruples uniquely determines a matrix A we have established
 \begin{align} \sharp \{ A\in M_{z,\star}^{(\lambda)}(r)\colon r\asymp K \} &\ll \frac{K^{\frac{1}{2}}}{p^{\lambda}y}\cdot K^{\frac{1}{2}}\cdot (1+\sqrt{K}y+\frac{Ky}{p^{\lambda}}) \nonumber \\ &\ll \frac{K}{p^{\lambda}}+\frac{K^{\frac{3}{2}}}{p^\lambda}+\frac{K^2}{p^{2\lambda}}.\nonumber\end{align}
\begin{align} \sharp \{ A\in M_{z,\star}^{(\lambda)}(r)\colon r\asymp K \} &\ll \frac{K^{\frac{1}{2}}}{p^{\lambda}y}\cdot K^{\frac{1}{2}}\cdot (1+\sqrt{K}y+\frac{Ky}{p^{\lambda}}) \nonumber \\ &\ll \frac{K}{p^{\lambda}}+\frac{K^{\frac{3}{2}}}{p^\lambda}+\frac{K^2}{p^{2\lambda}}.\nonumber\end{align}
The case when we are only considering square matrices only needs a minor modification. Indeed, instead of counting
![]() $a+d$
trivially as earlier we observe that
$a+d$
trivially as earlier we observe that
If the matrix is parabolic the right-hand side would be 0. Thus we now consider only generic matrices. For those we can fix the left-hand side first, so that we determine
![]() $(a+d,\sqrt{r})$
essentially as solutions to a generalised Pell equation. There are at most
$(a+d,\sqrt{r})$
essentially as solutions to a generalised Pell equation. There are at most
![]() $\ll K^{\epsilon}$
possibilities.
$\ll K^{\epsilon}$
possibilities.
Lemma 4·6. We have
 \begin{align} &\sum_{l\in S}M_{z,u}^{(\lambda)}(l) \ll \Lambda+\frac{\Lambda^{\frac{3}{2}} y}{p^{\lambda}}, \nonumber \\ &\sum_{l_1,l_2\in S}M_{z,u}^{(\lambda)}(l_1l_2) \ll \Lambda^2+\frac{\Lambda^3y}{p^{\lambda}} \text{ and }\nonumber\\ &\sum_{l_1,l_2\in S}M_{z,u}^{(\lambda)}(l_1^2l_2^2) \ll \Lambda^2+\frac{\Lambda^{4}y}{p^{\lambda}}.\nonumber\end{align}
\begin{align} &\sum_{l\in S}M_{z,u}^{(\lambda)}(l) \ll \Lambda+\frac{\Lambda^{\frac{3}{2}} y}{p^{\lambda}}, \nonumber \\ &\sum_{l_1,l_2\in S}M_{z,u}^{(\lambda)}(l_1l_2) \ll \Lambda^2+\frac{\Lambda^3y}{p^{\lambda}} \text{ and }\nonumber\\ &\sum_{l_1,l_2\in S}M_{z,u}^{(\lambda)}(l_1^2l_2^2) \ll \Lambda^2+\frac{\Lambda^{4}y}{p^{\lambda}}.\nonumber\end{align}
Proof. The first estimate follows analogously to [
Reference Iwaniec and Sarnak14
, (A·10)] using
![]() $p^\lambda\mid b$
. Recall the bound
$p^\lambda\mid b$
. Recall the bound
![]() $\lvert{b}\rvert\ll \sqrt{r}y$
used in the process.
$\lvert{b}\rvert\ll \sqrt{r}y$
used in the process.
The other bounds are derived elementary using only the fact that S contains only primes. (In contrast to [ Reference Harcos and Templier11 , lemma 2·4] we do not need a lattice counting argument, because we have an additional congruence condition on b that we can use.) We will only show the final estimate, since the others are derived similarly.
There are
![]() $\ll \Lambda^2$
possible choices for
$\ll \Lambda^2$
possible choices for
![]() $r=l_1^2l_2^2\asymp \Lambda^4$
. Having fixed the determinant of this form we find that there are only
$r=l_1^2l_2^2\asymp \Lambda^4$
. Having fixed the determinant of this form we find that there are only
![]() $\ll 1$
choices for (a,d) with
$\ll 1$
choices for (a,d) with
![]() $ad=l_1^2l_2^2$
. Finally we observe that we can choose b in
$ad=l_1^2l_2^2$
. Finally we observe that we can choose b in
![]() $\ll 1+{\Lambda^2y}/{p^{\lambda}}$
ways, since
$\ll 1+{\Lambda^2y}/{p^{\lambda}}$
ways, since
![]() $p^\lambda\mid b$
and
$p^\lambda\mid b$
and
![]() $\lvert{b}\rvert\ll \Lambda^2 y$
. Putting these estimates together completes the proof.
$\lvert{b}\rvert\ll \Lambda^2 y$
. Putting these estimates together completes the proof.
Remark 4·7. Suppose
![]() $y\geq {\sqrt{3}}/{2}$
. As in [
Reference Iwaniec and Sarnak14
, (A.7)] we have the bound
$y\geq {\sqrt{3}}/{2}$
. As in [
Reference Iwaniec and Sarnak14
, (A.7)] we have the bound
 \begin{equation} \lvert{c}\rvert\leq \frac{\sqrt{8r}}{y} \leq \sqrt{\frac{2^5r}{3}}. \end{equation}
\begin{equation} \lvert{c}\rvert\leq \frac{\sqrt{8r}}{y} \leq \sqrt{\frac{2^5r}{3}}. \end{equation}
Thus if
![]() $p^{\lambda}\geq 3,5\cdot\sqrt{r}$
, we must have
$p^{\lambda}\geq 3,5\cdot\sqrt{r}$
, we must have
![]() $c=0$
. This is because
$c=0$
. This is because
![]() $p^{\lambda}\mid c$
. In this case we obtain
$p^{\lambda}\mid c$
. In this case we obtain
Finally we need to consider the parabolic contribution.
Lemma 4·8. For
![]() $\lambda\geq 1$
and
$\lambda\geq 1$
and
![]() $y\geq {\sqrt{3}}/{2}$
we have
$y\geq {\sqrt{3}}/{2}$
we have
 \begin{equation} \sum_{\substack{r\asymp K, \\ r=\square}} \sharp M_{z,p}^{(\lambda)}(r) \ll \frac{K^{\frac{3}{2}}}{p^{\lambda}}.\nonumber\end{equation}
\begin{equation} \sum_{\substack{r\asymp K, \\ r=\square}} \sharp M_{z,p}^{(\lambda)}(r) \ll \frac{K^{\frac{3}{2}}}{p^{\lambda}}.\nonumber\end{equation}
Proof. This follows along the lines of [
Reference Blomer, Harcos, Maga and Milićević4
, lemma 14]. We provide some details for the convenience of the reader. Let
![]() $A=\left(\begin{matrix} a & b \\ c & d \end{matrix}\right)$
be a matrix contributing the the count
$A=\left(\begin{matrix} a & b \\ c & d \end{matrix}\right)$
be a matrix contributing the the count
![]() $M_{z,p}^{(\lambda)}(r)$
for some
$M_{z,p}^{(\lambda)}(r)$
for some
![]() $r\asymp K$
with
$r\asymp K$
with
![]() $r=\square$
. We start by recalling the bounds
$r=\square$
. We start by recalling the bounds
The first one is (10) and the second one follows from (9) when looking at the imaginary part.
Now, since A is parabolic, we must have
The latter equality can be rewritten as
This implies that, if c is fixed, then
![]() $a-d$
has a fixed divisor of size at least
$a-d$
has a fixed divisor of size at least
![]() $\sqrt{\vert c\vert}$
. We conclude that there are
$\sqrt{\vert c\vert}$
. We conclude that there are
![]() $\ll 1+{\sqrt{K}}/{\sqrt{\vert c\vert}}$
possible choices for
$\ll 1+{\sqrt{K}}/{\sqrt{\vert c\vert}}$
possible choices for
![]() $a-d$
. By summing over all possibilities for
$a-d$
. By summing over all possibilities for
![]() $c\neq 0$
and
$c\neq 0$
and
![]() $p^\lambda\mid c$
we find that
$p^\lambda\mid c$
we find that
Finally, note that
![]() $\vert a+d\vert = 2\sqrt{r} \asymp \sqrt{K}$
, so that there are
$\vert a+d\vert = 2\sqrt{r} \asymp \sqrt{K}$
, so that there are
![]() $\ll \sqrt{K}$
possible choices for
$\ll \sqrt{K}$
possible choices for
![]() $a+d$
. Since
$a+d$
. Since
![]() $a-d$
and c determine b we are done after gathering all the contributions.
$a-d$
and c determine b we are done after gathering all the contributions.
We can now prove the main estimate of this section.
Lemma 4·9. Assume
![]() $p>3$
. Suppose
$p>3$
. Suppose
![]() $\pi$
belongs to Case 1, 2 or 3·1. Then, for
$\pi$
belongs to Case 1, 2 or 3·1. Then, for
![]() ${\sqrt{3}}/{2}\ll y\ll \sqrt{d}$
we have
${\sqrt{3}}/{2}\ll y\ll \sqrt{d}$
we have
If
![]() $\pi$
belongs to Case 3.2, then we have the weaker bound
$\pi$
belongs to Case 3.2, then we have the weaker bound
Proof. We start with Cases 1, 2 or 3·1. Our starting point is Corollary 4·3. Breaking the g-sum up into pieces on which we can estimate the character using Lemma 4·4 we get
 \begin{equation} \frac{(\sharp S)^2}{\dim_{\mathbb{C}}\pi_p^{K_p(m_{\pi})}} \cdot \Phi(z)^2 \ll T\sum_{0\leq \lambda \leq m_{\pi}}p^{\lambda} \sum_{r} \frac{\lvert{y_r}\rvert}{\sqrt{r}} \cdot \sharp M_z^{(\lambda)}(r).\nonumber\end{equation}
\begin{equation} \frac{(\sharp S)^2}{\dim_{\mathbb{C}}\pi_p^{K_p(m_{\pi})}} \cdot \Phi(z)^2 \ll T\sum_{0\leq \lambda \leq m_{\pi}}p^{\lambda} \sum_{r} \frac{\lvert{y_r}\rvert}{\sqrt{r}} \cdot \sharp M_z^{(\lambda)}(r).\nonumber\end{equation}
We first consider the contribution of
![]() $\lambda=0$
. In this case the counting problem is independent of p and relatively easy. Indeed we have
$\lambda=0$
. In this case the counting problem is independent of p and relatively easy. Indeed we have
This is for example [
Reference Templier23
, proposition 6·1] with
![]() $N=\delta=1$
and
$N=\delta=1$
and
![]() $z\in\mathcal{F}$
so that
$z\in\mathcal{F}$
so that
![]() $y\gg 1$
.
$y\gg 1$
.
Next we assume
![]() $\lambda>0$
. We summarise the results from Lemma 4·5, 4·8 and 4·6 in Table I below. Note that for the contribution of
$\lambda>0$
. We summarise the results from Lemma 4·5, 4·8 and 4·6 in Table I below. Note that for the contribution of
![]() $r=1$
we have used Remark 4·7.
$r=1$
we have used Remark 4·7.
Table 1. Summary of counting results

All together this gives a contribution of
Inserting these estimates in our (amplified) pre-trace inequality we get
 \begin{equation} \frac{(\sharp S)^2}{\dim_{\mathbb{C}}\pi_p^{K_p(m_{\pi})}} \cdot \Phi(z)^2 \ll T\left(\Lambda^4+\Lambda^{\frac{5}{2}}y+\sum_{1\leq \lambda \leq m_{\pi}}p^{\lambda}\left[\Lambda+\frac{\Lambda^4}{p^\lambda}+\frac{\Lambda^2y}{p^\lambda}\right]\right).\nonumber\end{equation}
\begin{equation} \frac{(\sharp S)^2}{\dim_{\mathbb{C}}\pi_p^{K_p(m_{\pi})}} \cdot \Phi(z)^2 \ll T\left(\Lambda^4+\Lambda^{\frac{5}{2}}y+\sum_{1\leq \lambda \leq m_{\pi}}p^{\lambda}\left[\Lambda+\frac{\Lambda^4}{p^\lambda}+\frac{\Lambda^2y}{p^\lambda}\right]\right).\nonumber\end{equation}
This simplifies to
Inserting
![]() $\Lambda=d^{\frac{1}{3}}$
yields
$\Lambda=d^{\frac{1}{3}}$
yields
which directly implies the result for the non-exceptional cases 1, 2 and 3·1.
Finally if
![]() $\pi$
belongs to Case 3·2, then the same analysis with the weaker character estimates yields
$\pi$
belongs to Case 3·2, then the same analysis with the weaker character estimates yields
 \begin{align} \frac{(\sharp S)^2}{\dim_{\mathbb{C}}\pi_p^{K_p(m_{\pi})}} \cdot \Phi(z)^2 &\ll T\left(d^{\frac{1}{2}}\Lambda^4+d^{\frac{1}{2}}\Lambda^{\frac{5}{2}}y+\sum_{1\leq \lambda \leq m_{\pi}}p^{\frac{m_{\pi}+\lambda}{2}}\left[\Lambda+\frac{\Lambda^4}{p^\lambda}+\frac{\Lambda^2y}{p^\lambda}\right]\right) \nonumber \\ &\ll T\left(d^{\frac{1}{2}}\Lambda^4+d^{\frac{1}{2}}\Lambda^{\frac{5}{2}}y + \Lambda d^{1+\epsilon}\right). \nonumber\end{align}
\begin{align} \frac{(\sharp S)^2}{\dim_{\mathbb{C}}\pi_p^{K_p(m_{\pi})}} \cdot \Phi(z)^2 &\ll T\left(d^{\frac{1}{2}}\Lambda^4+d^{\frac{1}{2}}\Lambda^{\frac{5}{2}}y+\sum_{1\leq \lambda \leq m_{\pi}}p^{\frac{m_{\pi}+\lambda}{2}}\left[\Lambda+\frac{\Lambda^4}{p^\lambda}+\frac{\Lambda^2y}{p^\lambda}\right]\right) \nonumber \\ &\ll T\left(d^{\frac{1}{2}}\Lambda^4+d^{\frac{1}{2}}\Lambda^{\frac{5}{2}}y + \Lambda d^{1+\epsilon}\right). \nonumber\end{align}
This prompts the choice
![]() $\Lambda=d^{\frac{1}{6}}$
and we find
$\Lambda=d^{\frac{1}{6}}$
and we find
This completes the proof.
Proof.
of Theorem 1·1: We are now ready to complete the proof of our main theorem. First of all note that it is enough to bound
![]() $\Phi(z)$
for
$\Phi(z)$
for
![]() $z\in\mathcal{F}$
. Next, if
$z\in\mathcal{F}$
. Next, if
![]() $y\ll \sqrt{d}$
(resp.
$y\ll \sqrt{d}$
(resp.
![]() $y\ll d^{\frac{1}{4}}$
), then we are done by the previous lemma. For larger y the Whittaker expansion (see Lemma 3·8) gives even better result.
$y\ll d^{\frac{1}{4}}$
), then we are done by the previous lemma. For larger y the Whittaker expansion (see Lemma 3·8) gives even better result.
Acknowledgements
I thank Prof. Dr. V. Blomer for fruitful discussions and useful comments on an earlier draft of this manuscript. I would also like to thank the anonymous referees for pointing out several oversights and inaccuracies.