Symmetric amenability and the nonexistence of Lie and Jordan derivations
Published online by Cambridge University Press: 24 October 2008
Extract
A. M. Sinclair has proved that if 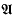 is a semisimple Banach algebra then every continuous Jordan derivation from
is a semisimple Banach algebra then every continuous Jordan derivation from 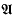 into
into 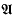 is a derivation ([12, theorem 3·3]; ‘Jordan derivation’ is denned in Section 6 below). If
is a derivation ([12, theorem 3·3]; ‘Jordan derivation’ is denned in Section 6 below). If 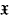 is a Banach
is a Banach 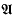 -bimodule one can consider Jordan derivations from
-bimodule one can consider Jordan derivations from 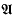 into
into 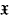 and ask whether Sinclair's theorem is still true. More recent work in this area appears in [1]. Simple examples show that it cannot hold for all modules and all semisimple algebras. However, for more restricted classes of algebras, including C*-algebras one does get a positive result and we develop two approaches. The first depends on symmetric amenability, a development of the theory of amenable Banach algebras which we present here for the first time in Sections 2, 3 and 4. A Banach algebra is symmetrically amenable if it has an approximate diagonal consisting of symmetric tensors. Most, but not all, amenable Banach algebras are symmetrically amenable and one can prove results for symmetric amenability similar to those in [8] for amenability. However, unlike amenability, symmetric amenability does not seem to have a concise homological characterisation. One of our results [Theorem 6·2] is that if
and ask whether Sinclair's theorem is still true. More recent work in this area appears in [1]. Simple examples show that it cannot hold for all modules and all semisimple algebras. However, for more restricted classes of algebras, including C*-algebras one does get a positive result and we develop two approaches. The first depends on symmetric amenability, a development of the theory of amenable Banach algebras which we present here for the first time in Sections 2, 3 and 4. A Banach algebra is symmetrically amenable if it has an approximate diagonal consisting of symmetric tensors. Most, but not all, amenable Banach algebras are symmetrically amenable and one can prove results for symmetric amenability similar to those in [8] for amenability. However, unlike amenability, symmetric amenability does not seem to have a concise homological characterisation. One of our results [Theorem 6·2] is that if 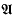 is symmetrically amenable then every continuous Jordan derivation into an
is symmetrically amenable then every continuous Jordan derivation into an 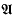 -bimodule is a derivation. Special techniques enable this result to be extended to other algebras, for example all C*-algebras. This approach to Jordan derivations appears in Section 6.
-bimodule is a derivation. Special techniques enable this result to be extended to other algebras, for example all C*-algebras. This approach to Jordan derivations appears in Section 6.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 120 , Issue 3 , October 1996 , pp. 455 - 473
- Copyright
- Copyright © Cambridge Philosophical Society 1996
References
REFERENCES
- 94
- Cited by


