No CrossRef data available.
Article contents
A table of n-component handlebody links of genus n+1 up to six crossings
Published online by Cambridge University Press: 17 June 2022
Abstract
A handlebody link is a union of handlebodies of positive genus embedded in 3-space, which generalises the notion of links in classical knot theory. In this paper, we consider handlebody links with a genus two handlebody and 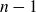 $n-1$ solid tori,
$n-1$ solid tori, 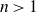 $n>1$. Our main result is the classification of such handlebody links with six crossings or less, up to ambient isotopy.
$n>1$. Our main result is the classification of such handlebody links with six crossings or less, up to ambient isotopy.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 174 , Issue 1 , January 2023 , pp. 199 - 223
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society
References
Bellettini, G., Paolini, M. and Wang, Y.-S.. Numerical irreducibility criteria for handlebody links. Topology Appl. 284 (2020), 107361, 14 pp.CrossRefGoogle Scholar
Botermans, J. and Van Delft, P.. Creative Puzzles of the World (Abrams, New York, 1975).Google Scholar
Brown, M.. Locally flat imbeddings of topological manifolds. Ann. Math., Second Series. 75, (1962), 331–341.CrossRefGoogle Scholar
Conway, J. H.. An enumeration of knots and links, and some of their algebraic properties, In Computational Problem in Abstract Algebra. Proc. Conf. Oxford. (1970), 329–358.CrossRefGoogle Scholar
Chongchitmate, W. and Ng, L.. An atlas of Legendrian knots. Exp. Math. 22 (2013), no. 1, 26–37.Google Scholar
Grushko, I. A.. On the bases of a free product of groups. Matematicheskii Sbornik. 8 (1940), 169–182.Google Scholar
Hirsch, M. W. and Mazur, B..
Smoothings of Piecewise Linear Manifolds
, (AM-80) (Princeton University Press, Princeton, NJ, 1974).Google Scholar
Hoste, J., Thistlethwaite, M. and Weeks, J.. The first 1,701,936 knots. Math. Intelligencer 20 (1998), 33–48.CrossRefGoogle Scholar
Ishii, A.. Moves and invariants for knotted handlebodies. Algebr. Geom Topol. 8 (2008), 1403–1418.CrossRefGoogle Scholar
Ishii, A. and Iwakiri, M.. Quandle cocycle invariants for spatial graphs and knotted handlebodies. Canad. J. Math. 64 (2012), 102–122.Google Scholar
Ishii, A., Iwakiri, M., Jang, Y. and Oshiro, K.. A G-family of quandles and handlebody-knots. Illinois J. Math. 57 (2013), 817–838.Google Scholar
Ishii, A., Kishimoto, K., Moriuchi, H. and Suzuki, M.. A table of genus two handlebody-knots up to six crossings. J. Knot Theory Ramifications 21 (2012), no. 4, 1250035, 9 pp.CrossRefGoogle Scholar
Ishii, A., Kishimoto, K. and Ozawa, M.. Knotted handle decomposing spheres for handlebody-knots. J. Math. Soc. Japan 67 (2015), 407–417.Google Scholar
Kauffman, L. H.. Invariants of graphs in three-space. Trans. Amer. Math. Soc. 311 (1989), no. 2, 679–710.Google Scholar
Kitano, T. and Suzuki, M.. On the number of
 $SL(2,\mathbb{Z}/p\mathbb{Z})$
-representations of knot groups. J. Knot Theory Ramifications. 21 (2012), no. 1, 1250003, 18 pp.CrossRefGoogle Scholar
$SL(2,\mathbb{Z}/p\mathbb{Z})$
-representations of knot groups. J. Knot Theory Ramifications. 21 (2012), no. 1, 1250003, 18 pp.CrossRefGoogle Scholar
Koda, Y. and Ozawa, M., with an appendix by C. Gordon. Essential surfaces of non-negative Euler characteristic in genus two handlebody exteriors. Trans. Amer. Math. Soc. 367 (2015), no. 4, 2875–2904.CrossRefGoogle Scholar
Lackenby, M.. The crossing number of composite knots. J. Topol. 2 (4) (2009), 747–768.CrossRefGoogle Scholar
Lee, J. H. and Lee, S.. Inequivalent handlebody-knots with homeomorphic complements. Algebr. Geom. Topol. 12 (2012), 1059–1079.CrossRefGoogle Scholar
Malyutin, A. V.. On the question of genericity of hyperbolic knots. Int. Math. Res. Notices. (2018), 1073–7928.Google Scholar
Mizusawa, A.. Linking numbers for handlebody-links. Proc. Japan Acad. 89, Ser. A (2013), 60–62.CrossRefGoogle Scholar
Moriuchi, H.. An enumeration of theta-curves with up to seven crossings. J. Knot Theory Ramifications. 18 (2009), 67–197.Google Scholar
Moriuchi, H.. A table of handcuff graphs with up to seven crossings. OCAMI Studies Vol 1. Knot Theory for Scientific objects
(2007), 179–300.Google Scholar
Moriuchi, H.. A table of
 $\theta$
-curves and handcuff graphs with up to seven crossings. Adv. Stud. Pure Math. Noncommutativity and Singularities: Proceedings of French–Japanese symposia held at IHES in 2006, J.-P. Bourguignon, M. Kotani, Y. Maeda and N. Tose, eds. (Tokyo: Mathematical Society of Japan, 2009), 281–290.Google Scholar
$\theta$
-curves and handcuff graphs with up to seven crossings. Adv. Stud. Pure Math. Noncommutativity and Singularities: Proceedings of French–Japanese symposia held at IHES in 2006, J.-P. Bourguignon, M. Kotani, Y. Maeda and N. Tose, eds. (Tokyo: Mathematical Society of Japan, 2009), 281–290.Google Scholar
Motto, M.. Inequivalent genus two handlebodies in
 $S^{3}$
with homeomorphic complements. Topology Appl. 36(3) (1990), 283–290.CrossRefGoogle Scholar
$S^{3}$
with homeomorphic complements. Topology Appl. 36(3) (1990), 283–290.CrossRefGoogle Scholar
Munkres, J..
Elementary Differential Topology
, (AM-54). (Princeton University Press, Princeton, NJ, 1966).Google Scholar
Paolini, M.. Appcontour. Computer software. Vers. 2.5.3. Apparent contour, (2018)
 $<$
http://appcontour.sourceforge.net/
$<$
http://appcontour.sourceforge.net/
 $>$
.$+.>Google Scholar
$>$
.$+.>Google Scholar
Rourke, C. P. and Sanderson, B. J.. Introduction to Piecewise-Linear Topology. (Springer-Verlag, Berlin-New York, 1982).Google Scholar
Suzuki, S., On surfaces in 3-sphere: prime decompositions. Hokkaido Math. J. 4 (1975), 179–195.CrossRefGoogle Scholar
Tsukui, Y., On a prime surface of genus 2 and homeomorphic splitting of 3-sphere. Yokohama Math. J. 23 (1975), 63–75.Google Scholar
Whitney, H., Congruent graphs and the connectivity of graphs. Amer. J. Math. 54 (1932), 150–168.CrossRefGoogle Scholar
Yetter, D. N., Category theoretic representations of knotted graphs in
 $S^3$
. Adv. Math. 77 (1989), 137–155.CrossRefGoogle Scholar
$S^3$
. Adv. Math. 77 (1989), 137–155.CrossRefGoogle Scholar

