Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Barbour, Andrew D.
1975.
The asymptotic behaviour of birth and death and some related processes.
Advances in Applied Probability,
Vol. 7,
Issue. 1,
p.
28.
Barbour, Andrew D.
1976.
Second order limit theorems for the Markov branching process in random environments.
Stochastic Processes and their Applications,
Vol. 4,
Issue. 1,
p.
33.
Heyde, C. C.
1977.
On the rate of convergence in the martingale convergence theorem.
Advances in Applied Probability,
Vol. 9,
Issue. 2,
p.
196.
Heyde, C. C.
1977.
On central limit and iterated logarithm supplements to the martingale convergence theorem.
Journal of Applied Probability,
Vol. 14,
Issue. 4,
p.
758.
Heyde, C. C.
1977.
On the rate of convergence in the martingale convergence theorem.
Advances in Applied Probability,
Vol. 9,
Issue. 2,
p.
196.
Heyde, C. C.
1977.
On central limit and iterated logarithm supplements to the martingale convergence theorem.
Journal of Applied Probability,
Vol. 14,
Issue. 4,
p.
758.
Asmussen, Søren
1977.
Almost sure behavior of linear functionals of supercritical branching processes.
Transactions of the American Mathematical Society,
Vol. 231,
Issue. 1,
p.
233.
Hall, Peter
1978.
Representations and limit theorems for extreme value distributions.
Journal of Applied Probability,
Vol. 15,
Issue. 3,
p.
639.
Loynes, R. M.
1978.
On the weak convergence of U-statistic processes, and of the empirical process.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 83,
Issue. 2,
p.
269.
Hall, Peter
1978.
Representations and limit theorems for extreme value distributions.
Journal of Applied Probability,
Vol. 15,
Issue. 03,
p.
639.
Kesten, Harry
1979.
The speed of convergence of a martingale.
Israel Journal of Mathematics,
Vol. 32,
Issue. 1,
p.
83.
Huggins, R. M.
1985.
On functional laws of the iterated logarithm.
Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 69,
Issue. 2,
p.
243.
Clark, J. M. C.
1987.
Convergent martingales of asymptotically minimal fluctuation.
Probability Theory and Related Fields,
Vol. 75,
Issue. 4,
p.
531.
Rosalsky, Andrew
and
Rosenblatt, Joseph
1998.
On convergence of series of random variables with applications to martingale convergence and to convergence of series with orthogonal summands.
Stochastic Analysis and Applications,
Vol. 16,
Issue. 3,
p.
553.
Nam, Eunwoo
Rosalsky, Andrew
and
Volodin, Andrej I.
1999.
On convergence of series of independent random elements in banach spaces.
Stochastic Analysis and Applications,
Vol. 17,
Issue. 1,
p.
85.
Rosalsky, Andrew
2007.
On the limiting behavior of tail series.
Journal of Statistical Planning and Inference,
Vol. 137,
Issue. 3,
p.
935.
Maller, Ross
2010.
Selected Works of C.C. Heyde.
p.
8.
Heyde, C. C.
2010.
Selected Works of C.C. Heyde.
p.
321.
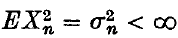 and assume that
and assume that 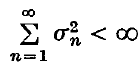 then
then 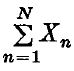 converges almost surely as N → ∞. Let
converges almost surely as N → ∞. Let 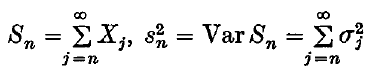 and let Fn(x) denote the distribution function of Xn. Loynes (2) observed that the sequence {Sn} is a reversed martingale, and applied his central limit theorem to it: however, stronger results are obtainable, in precise duality with the classical theory of partial sums of independent random variables. These results describe the fluctuations of the sequence {Sn}, and hence the way in which
and let Fn(x) denote the distribution function of Xn. Loynes (2) observed that the sequence {Sn} is a reversed martingale, and applied his central limit theorem to it: however, stronger results are obtainable, in precise duality with the classical theory of partial sums of independent random variables. These results describe the fluctuations of the sequence {Sn}, and hence the way in which 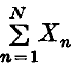 converges to its limit.
converges to its limit.