Published online by Cambridge University Press: 24 October 2008
1. In the Lehrbuch der abzählenden Methoden Zeuthen considers the problem of determining the nature and multiplicity of the tangent lines and planes to a degenerate surface in ordinary space. The surface φ in question consists of n arbitrary planes; these meet in pairs, forming 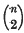 double lines, and in threes, forming
double lines, and in threes, forming 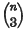 triple points. The tangent cone to φ from an arbitrary point consists of
triple points. The tangent cone to φ from an arbitrary point consists of 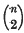 plane pencils, each counted twice, as follows from the known theory of degenerate plane curves. According to Zeuthen the tangent planes are of two types:
plane pencils, each counted twice, as follows from the known theory of degenerate plane curves. According to Zeuthen the tangent planes are of two types:
(i) those passing through one of the triple points; there are thus 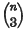 such systems, and each is to be counted six times;
such systems, and each is to be counted six times;
(ii) those passing through certain points S lying on the double lines; these depend upon the passage to the limit, it being assumed that φ is obtained as the limiting form of some nondegenerate surface. Two such points lie on each double line, so that there are n(n−1) such systems of planes.
* Zeuthen, , Lehrbuch der abzählenden Methoden der Geometrie (1914), p. 48.Google Scholar
* Cf. Salmon, , Higher Plane Curves (4th edn.), § 241.Google Scholar