Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hewitt, Edwin
and
Ross, Kenneth A.
1965.
Extensions of Haar measure and of harmonic analysis for locally compact Abelian groups.
Mathematische Annalen,
Vol. 160,
Issue. 3,
p.
171.
Peterson, H. Leroy
1977.
Extensions of Haar measure to relatively large nonmeasurable subgroups.
Transactions of the American Mathematical Society,
Vol. 228,
Issue. 0,
p.
359.
COMFORT, W.W.
1984.
Handbook of Set-Theoretic Topology.
p.
1143.
Kakutani, Shizuo
Anzai, Hirotada
Kodaira, Kunihiko
and
Hewitt, Edwin
1986.
Shizuo Kakutani.
p.
59.
ITZKOWITZ, GERALD L.
1992.
Pseudocompactness, Measurability, and Category in Compact Groups.
Annals of the New York Academy of Sciences,
Vol. 659,
Issue. 1,
p.
111.
Hart, Joan E.
and
Kunen, Kenneth
2006.
Limits in compact Abelian groups.
Topology and its Applications,
Vol. 153,
Issue. 7,
p.
991.
Defant, Andreas
and
Schoolmann, Ingo
2019.
$$\pmb {{\mathcal {H}}_{p}}$$-Theory of General Dirichlet Series.
Journal of Fourier Analysis and Applications,
Vol. 25,
Issue. 6,
p.
3220.


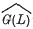 will denote the character group with the usual Pontrjagin topology (which is locally compact).
will denote the character group with the usual Pontrjagin topology (which is locally compact). 