Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Barbour, A. D.
1982.
Poisson convergence and random graphs.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 92,
Issue. 2,
p.
349.
Oxley, James G.
1984.
Threshold distribution functions for some random representable matroids.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 95,
Issue. 2,
p.
335.
Györi, E.
Rothschild, B.
and
Runciński, A.
1985.
Every graph is contained in a sparsest possible balanced graph.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 98,
Issue. 3,
p.
397.
Rucińiski, Andrzej
1985.
Random Graphs '83, Based on lectures presented at the 1st Poznań Seminar on Random Graphs.
Vol. 118,
Issue. ,
p.
221.
Ruciński, Andrzej
and
Vince, Andrew
1986.
Strongly balanced graphs and random graphs.
Journal of Graph Theory,
Vol. 10,
Issue. 2,
p.
251.
Ruciński, Andrzej
1988.
When are small subgraphs of a random graph normally distributed?.
Probability Theory and Related Fields,
Vol. 78,
Issue. 1,
p.
1.
Nowicki, Krzysztof
and
Wierman, John C.
1988.
Subgraph counts in random graphs using incomplete u-statistics methods.
Discrete Mathematics,
Vol. 72,
Issue. 1-3,
p.
299.
Nowicki, Krzysztof
and
Wierman, John C.
1988.
Graph Theory and Applications, Proceedings of the First Japan Conference on Graph Theory and Applications.
Vol. 38,
Issue. ,
p.
299.
Nowicki, Krzysztof
1988.
Asymptotic Poisson distributions with applications to statistical analysis of graphs.
Advances in Applied Probability,
Vol. 20,
Issue. 2,
p.
315.
Nowicki, Krzysztof
1988.
Asymptotic Poisson distributions with applications to statistical analysis of graphs.
Advances in Applied Probability,
Vol. 20,
Issue. 2,
p.
315.
Nowicki, Krzysztof
1989.
Asymptotic normality of triad counts in random digraphs.
Communications in Statistics. Stochastic Models,
Vol. 5,
Issue. 2,
p.
163.
RUCIŃSKI, ANDRZEJ
and
VINCE, ANDREW
1989.
Balanced Extensions of Graphs.
Annals of the New York Academy of Sciences,
Vol. 555,
Issue. 1,
p.
347.
PALKA, ZBIGNIEW
1989.
Orders of Induced Subgraphs in Sparse Random Graphs.
Annals of the New York Academy of Sciences,
Vol. 576,
Issue. 1,
p.
431.
KAROŃSKI, MICHAL
and
RUCIŃSKI, ANDRZEJ
1989.
Small Subgraphs of k‐Partite Random Graphs.
Annals of the New York Academy of Sciences,
Vol. 555,
Issue. 1,
p.
230.
BOLLOBÁS, BÉLA
and
WIERMAN, JOHN C.
1989.
Subgraph Counts and Containment Probabilities of Balanced and Unbalanced Subgraphs in a Large Random Grapha.
Annals of the New York Academy of Sciences,
Vol. 576,
Issue. 1,
p.
63.
Suen, W. C. Stephen
1990.
A correlation inequality and a poisson limit theorem for nonoverlapping balanced subgraphs of a random graph.
Random Structures & Algorithms,
Vol. 1,
Issue. 2,
p.
231.
Ruciński, Andrzej
1992.
Matching and covering the vertices of a random graph by copies of a given graph.
Discrete Mathematics,
Vol. 105,
Issue. 1-3,
p.
185.
Ruciński, A.
and
Vince, A.
1993.
The solution to an extremal problem on balanced extensions of graphs.
Journal of Graph Theory,
Vol. 17,
Issue. 3,
p.
417.
Ruciński, Andrzej
1993.
Quo Vadis, Graph Theory? - A Source Book for Challenges and Directions.
Vol. 55,
Issue. ,
p.
265.
Roberts, Fred S.
1993.
Quo Vadis, Graph Theory? - A Source Book for Challenges and Directions.
Vol. 55,
Issue. ,
p.
13.
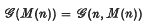
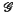 (M(n)) into a probability space by giving all graphs the same probability. The question we address ourselves to is the following. Given a graph H and a constant p, 0 < p < 1, for what functions M(n) is it true that the probability PM(n)(H ⊂ G) that a graph G∈
(M(n)) into a probability space by giving all graphs the same probability. The question we address ourselves to is the following. Given a graph H and a constant p, 0 < p < 1, for what functions M(n) is it true that the probability PM(n)(H ⊂ G) that a graph G∈ 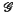 (M(n)) contains H tends to p as n∞→? This question was posed by Erdös and Rényi (3), (4), who also proved several beautiful and surprising theorems. In order to state the main general result of Erdös and Rényi in this direction, and for our use later, we introduce some definitions.
(M(n)) contains H tends to p as n∞→? This question was posed by Erdös and Rényi (3), (4), who also proved several beautiful and surprising theorems. In order to state the main general result of Erdös and Rényi in this direction, and for our use later, we introduce some definitions.