Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T16:29:46.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Topos points of quasi-coherent sheaves over monoid schemes

Part of: Special categories Semigroups

Published online by Cambridge University Press:  11 March 2019

ILIA PIRASHVILI
ILIA PIRASHVILI*
Affiliation:
Institute for Mathematics, University of Osnabrück, Albrechtstr. 28a, D-49069, Germany. email: ilia.pirashvili@uni-osnabrueck.de (ilia_p@ymail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let X be a monoid scheme. We will show that the stalk at any point of X defines a point of the topos 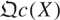of quasi-coherent sheaves over X. As it turns out, every topos point of 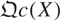is of this form if X satisfies some finiteness conditions. In particular, it suffices for M/M× to be finitely generated when X is affine, where M× is the group of invertible elements.

This allows us to prove that two quasi-projective monoid schemes X and Y are isomorphic if and only if 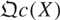and 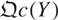are equivalent.

The finiteness conditions are essential, as one can already conclude by the work of A. Connes and C. Consani [3]. We will study the topos points of free commutative monoids and show that already for ℕ∞, there are ‘hidden’ points. That is to say, there are topos points which are not coming from prime ideals. This observation reveals that there might be a more interesting ‘geometry of monoids’.

MSC classification

Primary: 18B25: Topoi
Secondary: 20M14: Commutative semigroups 20M30: Representation of semigroups; actions of semigroups on sets
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 169 , Issue 1 , July 2020 , pp. 31 - 74
Copyright
© Cambridge Philosophical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abramovich, D., Chen, Q., Gillam, D., Huang, Y., Olsson, M., Satriano, M., and Sun, S.. Logarithmic geometry and moduli. arXiv:1006.5870. (2010).Google Scholar
Chu, C., Lorscheid, O. and Santhanam, R.. Sheaves and K-theory for -schemes. Adv. Math. 229, (2012), p. 2239–2286.CrossRefGoogle Scholar
Connes, A.. and Consani, C.. Geometry of the arithmetic site. Adv. Math. 291, (2016), p. 274–329.CrossRefGoogle Scholar
Connes, A.. and Consani, C.. Schemes over and zeta functions. Compositio Mathematica 146.6, (2010), p. 1383–1415.CrossRefGoogle Scholar
Cortinas, G., Haesemeyer, C., Walker, M. E. and Weibel, C.. Toric variaties, monoid schemes and cdh descent. J. für die Reine u Angewan. Math. 698 (2015), p. 1–54.Google Scholar
Deitmar, A.. Schemes over . In: Number fields and function field. Two parallel worlds. Ed. by van der Geer, G., Moonen, B., Schoof, R.. Progr. in Math. (2005), 236.Google Scholar
Gabriel, P.. Des catégories abéliennes. Bull. Soc. Math. France 90 (1962), p. 323–448.CrossRefGoogle Scholar
Garkusha, G. and Prest, M.. Reconstructing projective schemes from Serre subcategories. J. Algebra 319 no. 3 (2008), p. 1132–1153.CrossRefGoogle Scholar
Gilmer, R.. Commutative Semigroup Rings. (The University of Chicago Press 1984).Google Scholar
Kato, K.. Toric singularities. Ameri. J. Math. 11 6. (1994), p. 1073–1099.CrossRefGoogle Scholar
Kato, K.. Logarithmic structures of Fontaine-Illusie, in Algebraic Analysis, Geometry, and Number Theory. Proceedings of the JAMI Inaugural Conference. Supplement to Amer. J. Math., (1989), p. 191–224.Google Scholar
Mac Lane, S. and Moerdijk, I.. Sheaves in Geometry and Logic. A First Introduction to Topos Theory. Corrected reprint of the 1992 edition. Universitext. (Springer-Verlag, New York, 1994).CrossRefGoogle Scholar
Moerdijk, I.. Classifying Spaces and Classifying Topoi. Lecture Notes in Mathe. vol. 1616, Springer-Verlag, Berlin, (1995).CrossRefGoogle Scholar
Pin, J.E.. Tropical semirings. Idempotency (Bristol, 1994) Publ. Newton Inst., 11, (Cambridge University Press, Cambridge, 1998), p. 50–59.CrossRefGoogle Scholar
Pirashvili, I.. On the spectrum of monoids and semilattices. J. Pure Appl. Algebra 217 (2013), p. 901–906.CrossRefGoogle Scholar
Pirashvili, I.. On cohomology and vector bundles over monoid schemes. J. Algebra 435 (2015), p. 33–51.Google Scholar
Rosenberg, A. L.. The spectrum of abelian categories and reconstruction of schemes. Rings, Hopf algebras and Brauer groups (Antwerp/Brussels 1996) Lecture Notes in Pure and Appl. Math. 197 (1998), p. 257–274.Google Scholar