Published online by Cambridge University Press: 24 October 2008
Let M be a closed simply-connected 4-manifold. All manifolds will be assumed smooth and oriented. The purpose of this paper is to classify up to conjugacy the topological subgroups of Diff(M) isomorphic to the 2-dimensional torus T2 (Theorem 1), and to give an explicit formula for the number of such conjugacy classes (Theorem 2). Such a conjugacy class corresponds uniquely to a weak equivalence class of effective T2-actions on M. Thus the classification problem is trivial unless M supports an effective T2-action. Orlik and Raymond showed that this happens if and only if M is a connected sum of copies of ± 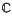 ;P2 and S2 × S2 (2), and so this paper is really a study of the different T2-actions on these manifolds.
;P2 and S2 × S2 (2), and so this paper is really a study of the different T2-actions on these manifolds.