Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-24T12:14:23.887Z Has data issue: false hasContentIssue false
  • English
  • Français

Torsion classes in the cohomology of congruence subgroups

Published online by Cambridge University Press:  24 October 2008

Dominique Arlettaz
Dominique Arlettaz
Affiliation:
Département de Mathématiques, Ecole Polytechnique Fédérate, CH-1015 Lausanne, Switzerland
Get access Rights & Permissions [Opens in a new window]

Extract

For any prime number p, let Γn, p denote the congruence subgroup of SLn(ℤ) of level p, i.e. the kernel of the surjective homomorphism fp: SLn(ℤ) → SLn(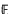p) induced by the reduction mod p (Fp is the field with p elements). We define

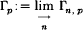
using upper left inclusions Γn, p ↪ Γn+1, p. Recall that the groups Γn, p are homology stable with M-coefficients, for instance if M = ℚ, ℤ[1/p], or ℤ/q with q prime and q ╪ p: Hi(Γn, p; M) ≅ Hi(Γp; M) for n ≥ 2i + 5 from [7] (but the homology stability fails if M = ℤ or ℤ/p).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 105 , Issue 2 , March 1989 , pp. 241 - 248
Copyright
Copyright © Cambridge Philosophical Society 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Arlettaz, D.. Sur les classes de Stiefel–Whitney des sous-groupes de congruence. C. R. Acad. Sci. Paris Sér. I Math. 303 (1986), 571–574.Google Scholar
[2]Arlettaz, D.. On the homology and cohomology of congruence subgroups. J. Pure Appl. Algebra 44 (1987), 3–12.Google Scholar
[3]Arlettaz, D.. On the k-invariants of iterated loop spaces. Proc. Roy. Soc. Edinburgh Sect. A. (To appear.)Google Scholar
[4]Bökstedt, M.. The rational homotopy type of ΩWh diff(*). In Algebraic Topology Aarhus 1982, Lecture Notes in Math. vol. 1051 (Springer-Verlag, 1984), pp. 25–37.Google Scholar
[5]Borel, A.. Topics in the Homology Theory of Fibre Bundles. Lecture Notes in Math. vol. 36 (Springer-Verlag, 1967).Google Scholar
[6]Cartan, H.. Algèbres d'Eilenberg–MacLane et Homotopie. Séminaire H. Cartan Ecole Norm. Sup. (1954/1955), expose 11.Google Scholar
[7]Charney, R.. On the problem of homology stability for congruence subgroups. Comm. Algebra 12 (1984), 2081–2123.Google Scholar
[8]Dwyer, W. G. and Friedlander, E. M.. Conjectural calculations of general linear group homology. In Applications of Algebraic K-theory to Algebraic Geometry and Number Theory, Contemp. Math. vol. 55 Part I (1986), pp. 135–147.Google Scholar
[9]Fiedorowicz, Z. and Priddy, S.. Homology of Classical groups over Finite Fields and their associated Infinite Loop Spaces. Lecture Notes in Math. vol. 674 (Springer-Verlag, 1978).Google Scholar
[10]Lee, R. and Szczarba, R. H.. On the homology and cohomology of congruence subgroups. Invent. Math. 33 (1976), 15–53.Google Scholar
[11]Millson, J. J.. Real vector bundles with discrete structure group. Topology 18 (1979), 83–89.Google Scholar
[12]Quillen, D.. On the cohomology and K-theory of the general linear groups over a finite field. Ann. of Math. (2) 96 (1972), 552–586.CrossRefGoogle Scholar
[13]Soulé, C.. K-théorie des anneaux d'entiers de corps de nombres et cohomologie étale. Invent. Math. 55 (1979), 251–295.Google Scholar
[14]Soulé, C.. Groupes de Chow et K-théorie de variétés sur un corps fini. Math. Ann. 268 (1984), 317–345.Google Scholar
[15]Thomas, E.. On the cohomology of the real Grassmann complexes and the characteristic classes of n-plane bundles. Trans. Amer. Math. Soc. 96 (1960), 67–89.Google Scholar
[16]Weintraub, S. H.. Which groups have strange torsion? In Tranformation Groups Poznań 1985, Lecture Notes in Math. vol. 1217 (Springer-Verlag, 1986), pp. 394–396.Google Scholar