Torsion of beams whose cross-section is a regular polygon of n sides
Published online by Cambridge University Press: 24 October 2008
Extract
E. Trefftz has discussed the problem of the torsion of a beam whose cross-section is bounded by a polygon with the help of the Schwarz-Christoffel transformation given by
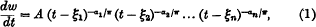
where a1, a2, …, an are external angles of the polygon in the w-plane, and ξ1, ξ2, …, ξn are the points on the real ξ-axis in the t-plane that correspond to the angular points of the polygon in the w-plane. In the case of regular polygons a further transformation of the upper half of the t-plane into the interior of a circle in the z-plane with the help of the transformation

greatly simplifies the problem, and some definite results can be obtained.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 30 , Issue 2 , 30 April 1934 , pp. 139 - 149
- Copyright
- Copyright © Cambridge Philosophical Society 1934
References
* Math. Ann. 82 (1921), 306–319.Google Scholar
* This result is due to Schwarz. See Forsyth, , Theory of functions, 3rd edition, p. 768, Ex. 2.Google Scholar
* Cf. Dixon, A. C., Quart. Journ. of Math. 24 (1890), 167–233.Google Scholar
* Richelot, , Journal für Math. 9 (1832), 407–408Google Scholar, also Cayley, , Proc. Camb. Phil. Soc. 4 (1881), 106–109.Google Scholar
* Thomson, and Tait, , Natural Philosophy, Vol. i, Part 2, pp. 249–250.Google Scholar
* That this supposition of Boussinesq is not always true has been shown by Filon, L. N. G., Phil. Trans. Roy. Soc. 193 (1900), 309–352.CrossRefGoogle Scholar
- 6
- Cited by


