Published online by Cambridge University Press: 24 October 2008
Let 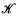 be an oriented knot in S3 and
be an oriented knot in S3 and 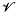 a solid torus endowed with a preferred framing which contains
a solid torus endowed with a preferred framing which contains 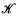 in its interior. By ρ and λ we denote the wrapping and winding numbers of
in its interior. By ρ and λ we denote the wrapping and winding numbers of 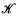 in
in 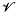 respectively. That is, they are the geometric and algebraic intersection numbers of
respectively. That is, they are the geometric and algebraic intersection numbers of 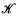 and a meridian disk of
and a meridian disk of 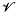 . For an integer μ, let τμ be an orientation-preserving homeomorphism of
. For an integer μ, let τμ be an orientation-preserving homeomorphism of 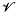 satisfying τμ(m) = m and τμ(l) = l + μm in H1(∂
satisfying τμ(m) = m and τμ(l) = l + μm in H1(∂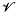 ), where (m, l) is a meridian-longitude pair of
), where (m, l) is a meridian-longitude pair of 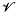 . We call τμ(
. We call τμ(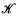 ), denoted by
), denoted by 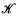 μ, the knot obtained from
μ, the knot obtained from 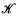 by μ-twisting along
by μ-twisting along 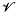 .
.