Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-26T06:40:30.530Z Has data issue: false hasContentIssue false
  • English
  • Français

Unconditionally converging polynomials on Banach spaces

Published online by Cambridge University Press:  24 October 2008

Manuel Gonz´lez  and
Joaquín M. Gutiérrez
Manuel Gonz´lez
Affiliation:
Departamento de Matemáticas, Facultad de Ciencias, Universidad de Cantabria, 39071 Santander, Spain
Joaquín M. Gutiérrez
Affiliation:
Departamento de Matemática Aplicada, ETS de Ingenieros Industriales, Universidad
Get access Rights & Permissions [Opens in a new window]

Extract

In the study of polynomials acting on Banach spaces, the weak topology is not such a good tool as in the case of linear operators, due to the bad behaviour of the polynomials with respect to the weak convergence. For example,

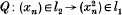
is a continuous polynomial taking a weakly null sequence into a sequence having no weakly Cauchy subsequences. In this paper we show that the situation is not so bad for unconditional series. Recall that 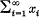is a weakly unconditionally Cauchy series (in short a w.u.C. series) in a Banach space E if for every f ε E* we have that 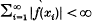and 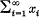is an unconditionally converging series (in short an u.c. series) if every subseries is norm convergent.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 117 , Issue 2 , March 1995 , pp. 321 - 331
Copyright
Copyright © Cambridge Philosophical Society 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Alencar, R., Aron, R. M. and Dineen, S.. A reflexive space of holomorphic functions in infinitely many variables. Proc. Amer. Math. Soc. 90 (1984), 407–411.CrossRefGoogle Scholar
[2]Andrews, K. T.. Dunford-Pettis sets in the space of Bochner integrable functions. Math. Ann. 241 (1979), 35–41.CrossRefGoogle Scholar
[3]Aron, R. M., Choi, Y. S. and Llavona, J. G.. Estimates by polynomials, preprint (1993).Google Scholar
[4]Aron, R. M. and Globevnik, J.. Analytic functions on c 0. Revista Matemática Univ. Complutense Madrid 2 (1989), 27–33.Google Scholar
[5]Cembranos, P.. The hereditary Dunford-Pettis property on C(K, E). Illinois J. Math. 31 (1987), 365–373.CrossRefGoogle Scholar
[6]Diestel, J.. Sequence and series in Banach spaces (Springer-Verlag, 1984).CrossRefGoogle Scholar
[7]González, M. and Gutiérrez, J. M.. Weakly continuous mappings on Banach spaces with the Dunford-Pettis property. J. Math. Anal. Appl. 173 (1993), 470–483.CrossRefGoogle Scholar
[8]Grothendieck, A.. Sur les applications linéaires faiblement compactes d'espaces du type C(K). Canad. J. Math. 5 (1953), 129–173.CrossRefGoogle Scholar
[9]Lindenstrauss, J. and Tzafriri, L.. Classical Banach spaces I. Sequence spaces (Springer-Verlag, 1977).Google Scholar
[10]Mujica, J.. Complex analysis in Banach spaces. Math. Studies no. 120 (North-Holland, 1986).Google Scholar
[11]Pelczynski, A.. A property of multilinear operations. Studia Math. 16 (1957), 173–182.CrossRefGoogle Scholar
[12]Pelczynski, A.. Banach spaces on which every unconditionally converging operator is weakly compact. Bull. Acad. Polon. Sci. 10 (1962), 641–648.Google Scholar
[13]Pelczynski, A.. On weakly compact polynomial operators on B-spaces with Dunford-Pettis property. Bull. Acad. Polon. Sci. 11 (1963), 371–378.Google Scholar
[14]Ryan, R. A.. Dunford-Pettis properties. Bull. Acad. Polon. Sci. 27 (1979), 373–379.Google Scholar
[15]Ryan, R. A.. Applications of topological tensor products to infinite dimensional holomorphy. Ph.D. Thesis, Trinity College, Dublin (1980).Google Scholar
[16]Ryan, R. A.. Weakly compact holomorphic mappings on Banach spaces. Pacific J. Math. 131 (1988), 179–190.CrossRefGoogle Scholar
[17]Tsirelson, B. S.. Not every Banach space contains an embedding of l p or c 0. Functional Anal. Appl. 8 (1974), 138–141.CrossRefGoogle Scholar