Published online by Cambridge University Press: 24 October 2008
In recent years, the Stone-Čech compactification of certain semigroups (e.g. discrete semigroups) has been an interesting semigroup compactification (i.e. a compact right semitopological semigroup which contains a dense continuous homomorphic image of the given semigroup) to study, because an Arens-type product can be introduced. If G is a non-compact and non-discrete locally compact abelian group, then it is not possible to introduce such a product into the Stone-Čech compactification βG of G (see [1]). However, let UC(G) be the Banach algebra of bounded uniformly continuous complex functions on G, and let UG be the spectrum of UC(G) with the Gelfand topology. If f∈ UC(G), then the functions f and fy defined on G by
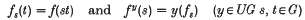
are also in UC(G).